
【题目】如图,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+b)2+|a-b+4|=0,过点C作CB⊥x轴于B.
(1)如图1,求△ABC的面积.
(2)如图2,若过B作BD∥AC交y轴于D,在△ABC内有一点E,连接AE.DE,若∠CAE+∠BDE=∠EAO+∠EDO,求∠AED的度数.
(3)如图3,在(2)的条件下,DE与x轴交于点M,AC与y轴交于点F,作△AME的角平分线MP,在PE上有一点Q,连接QM,∠EAM+2∠PMQ=45°,当AE=2AM,FO=2QM时,求点E的纵坐标.

【答案】(1)4;(2)45°;(3)1
【解析】
(1)由题意可求a=-2,b=2,即可得点A,点C坐标,即可求△ABC的面积;
(2)根据题意可求∠CAE+∠BDE=∠EAO+∠EDO=45°,根据三角形内角和可求∠AED的度数;
(3)如图3,先根据三角形的中位线定理可得:QM=![]() ,过E作EG⊥x轴于G,设∠PMQ=x,则∠EAM=45-2x,证明MQ⊥AE,利用面积法可得:S△AEM=
,过E作EG⊥x轴于G,设∠PMQ=x,则∠EAM=45-2x,证明MQ⊥AE,利用面积法可得:S△AEM=![]() AEMQ=
AEMQ=![]() AMEG,可得EG=1,即点E的纵坐标是1.
AMEG,可得EG=1,即点E的纵坐标是1.
(1)∵(a+b)2≥0,|a-b+4|≥0,(a+b)2+|a-b+4|=0,
∴a=-b,a-b+4=0,
∴a=-2,b=2,
∵CB⊥AB
∴A(-2,0),B(2,0),C(2,2),
∴△ABC的面积=![]() ×4×2=4;
×4×2=4;
(2)如图2,连接AD,
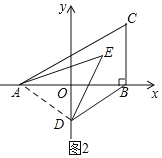
∵BD∥AC,
∴∠CAD+∠BDA=180°,
∵∠OAD+∠ODA=90°,
∴∠CAB+∠BDO=90°,
∵∠CAE+∠BDE=∠EAO+∠EDO,
∴∠CAE+∠BDE=∠EAO+∠EDO=45°,
△ADE中,∠AED=180°-(∠EAO+∠EDO)-(∠OAD+∠ODA)=180°-45°-90°=45°;
(3)如图3,
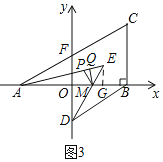
∵OF∥BC,OA=OB=2,
∴AF=FC,
∴OF=![]() BC=1,
BC=1,
∵OF=2QM,
∴QM=![]() ,
,
过E作EG⊥x轴于G,
设∠PMQ=x,则∠EAM=45-2x,
由(2)知:∠EAM+∠EDO=45°,
∴∠EDO=45°-(45°-2x)=2x,
∴∠EMG=∠OMD=90°-2x,
∵PM平分∠AME,
∴∠AMP=∠PME=![]() =45°+x,
=45°+x,
∴∠QPM=∠EAM+∠AMP=45°-2x+45°+x=90°-x,
∴∠QPM+∠PMQ=90°,
∴MQ⊥AE,
S△AEM=![]() AEMQ=
AEMQ=![]() AMEG,
AMEG,
∵AE=2AM,
∴2AM![]() =AMEG,
=AMEG,
∴EG=1,即点E的纵坐标是1.


科目:初中数学 来源: 题型:
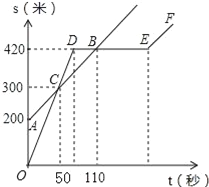
【题目】某中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动朱老师先跑,当小明出发时,朱老师已经距起点200米了,他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).根据图中给出的信息,解答下列问题:
(1)在上述变化过程中,自变量是 ,因变量是 ;
(2)朱老师的速度为 米/秒;小明的速度为 米/秒;
(3)小明与朱老师相遇 次,相遇时距起点的距离分别为 米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为直线x=![]() ,且经过点(2,0).下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(-2,y1),(
,且经过点(2,0).下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(-2,y1),(![]() ,y2)是抛物线上的两点,则y1<y2,其中说法正确的是( )
,y2)是抛物线上的两点,则y1<y2,其中说法正确的是( )
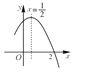
A. ①②④ B. ③④ C. ①③④ D. ①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN∥OP,点A为直线MN上一定点,B为直线OP上的动点,在直线MN与OP之间且在线段AB的右方作点D,使得AD⊥BD.设∠DAB=α(α为锐角).
(1)求∠NAD与∠PBD的和;(提示过点D作EF∥MN)
(2)当点B在直线OP上运动时,试说明∠OBD﹣∠NAD=90°;
(3)当点B在直线OP上运动的过程中,若AD平分∠NAB,AB也恰好平分∠OBD,请求出此时α的值

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() 中
中![]() ,
,![]() ,
,![]() .
.
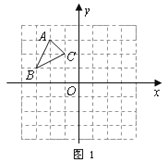
(1)将![]() 向右平移
向右平移![]() 个单位长度,画出平移后的
个单位长度,画出平移后的![]() ;
;
(2)画出![]() 关于
关于![]() 轴对称的
轴对称的![]() ;
;
(3)将![]() 绕原点
绕原点![]() 旋转
旋转![]() ,画出旋转后的
,画出旋转后的![]() ;
;
(4)在![]() ,
,![]() ,
,![]() 中,
中,
![]() ______与
______与![]() ______成轴对称,对称轴是______;
______成轴对称,对称轴是______;
![]() ______与
______与![]() ______成中心对称,对称中心的坐标是____.
______成中心对称,对称中心的坐标是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
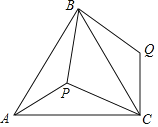
【题目】如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,若将△PAC绕点A逆时针旋转后得到△P′AB.
(1)求点P与点P′之间的距离;
(2)求∠APB的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长均为l的小正方形网格纸中,△ABC的顶点,A、B、C均在格点上,O为直角坐标系的原点,点A(-1,0)在x轴上.

(1)以O为位似中心,将△ABC放大,使得放大后的△A1B1C1与△ABC的相似比为2:1,要求所画△A1B1C1与△ABC在原点两侧;
(2)分别写出B1、C1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1 ,在矩形纸片![]() 中,
中,![]() ,折叠纸片使
,折叠纸片使![]() 点落在边
点落在边![]() 上的
上的![]() 处,折痕为
处,折痕为![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]()
![]() 求证:四边形
求证:四边形![]() 为菱形;
为菱形;
![]() 当点
当点![]() 在
在![]() 边上移动时,折痕的端点
边上移动时,折痕的端点![]() 也随之移动,若限定
也随之移动,若限定![]() 分别在边
分别在边![]() .上移动,求出点
.上移动,求出点![]() 在边
在边![]() 上移动的最大距离.
上移动的最大距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com