
【题目】如图,二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为直线x=![]() ,且经过点(2,0).下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(-2,y1),(
,且经过点(2,0).下列说法:①abc<0;②a+b=0;③4a+2b+c<0;④若(-2,y1),(![]() ,y2)是抛物线上的两点,则y1<y2,其中说法正确的是( )
,y2)是抛物线上的两点,则y1<y2,其中说法正确的是( )
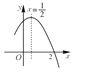
A. ①②④ B. ③④ C. ①③④ D. ①②
 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装着除颜色外完全相同的黑、白两种小球共40个,小明做摸球实验,他将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数m | 70 | 128 | 171 | 302 | 481 | 599 | 903 |
摸到白球的频率 | 0.75 | 0.64 | 0.57 | 0.604 | 0.601 | 0.599 | 0.602 |
(1)请估计:当n很大时,摸到白球的概率约为 .(精确到0.1)
(2)估算盒子里有白球 个.
(3)若向盒子里再放入x个除颜色以外其它完全相同的球,这x个球中白球只有1个,每次将球搅拌均匀后,任意摸出一个球记下颜色再放回,通过大量重复摸球试验后发现,摸到白球的频率稳定在50%,那么可以推测出x最有可能是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把y=![]() x2的图象向上平移2个单位.
x2的图象向上平移2个单位.
(1)求新图象的解析式、顶点坐标和对称轴;
(2)画出平移后的函数图象;
(3)求平移后的函数的最大值或最小值,并求对应的x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,![]() 中,
中,![]() ,求证:
,求证:![]() ;
;
(2)如图2,![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,垂足分别为
,垂足分别为![]() 、
、![]() ,
,![]() 与
与![]() 交于点
交于点![]() .试探究线段
.试探究线段![]() 与线段
与线段![]() 的数量关系.
的数量关系.
(3)如图3,![]() 中,
中,![]() ,
,![]() ,垂足为
,垂足为![]() ,若线段
,若线段![]() ,则
,则![]() 的面积为 .
的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广,为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写大赛”![]() 为了解本次大赛的成绩,校团委随机抽取了其中若干名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
为了解本次大赛的成绩,校团委随机抽取了其中若干名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
成绩 | 频数 | 频率 |
| 10 |
|
| 30 |
|
| 40 | n |
| m |
|
| 50 |
|
a | 1 |
请根据所给信息,解答下列问题:
![]() ______,
______,![]() ______,
______,![]() ______;
______;
![]() 补全频数直方图;
补全频数直方图;
![]() 这若干名学生成绩的中位数会落在______分数段;
这若干名学生成绩的中位数会落在______分数段;
![]() 若成绩在90分以上
若成绩在90分以上![]() 包括90分
包括90分![]() 的为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?
的为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
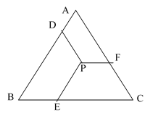
【题目】如图,已知等边△ABC的边长为10,P是△ABC内一点,PD平行AC,PE平行AD,PF平行BC,点D,E,F分别在AB,BC,AC上,则PD+PE+PF= _______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+b)2+|a-b+4|=0,过点C作CB⊥x轴于B.
(1)如图1,求△ABC的面积.
(2)如图2,若过B作BD∥AC交y轴于D,在△ABC内有一点E,连接AE.DE,若∠CAE+∠BDE=∠EAO+∠EDO,求∠AED的度数.
(3)如图3,在(2)的条件下,DE与x轴交于点M,AC与y轴交于点F,作△AME的角平分线MP,在PE上有一点Q,连接QM,∠EAM+2∠PMQ=45°,当AE=2AM,FO=2QM时,求点E的纵坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让市民享受到更多的优惠,相关部门拟确定一个折扣线,计划使50%左右的人获得折扣优惠.某市针对乘坐地铁的人群进行了调查.调查小组在各地铁站随机调查了该市1000人上一年乘坐地铁的月均花费(单位:元),绘制了频数分布直方图,如图所示.下列说法正确的是( )

①每人乘坐地铁的月均花费最集中的区域在80~100元范围内;
②每人乘坐地铁的月均花费的平均数范围是40~60元范围内;
③每人乘坐地铁的月均花费的中位数在60~100元范围内;
④乘坐地铁的月均花费达到80元以上的人可以享受折扣.
A.①②④B.①③④C.③④D.①②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com