
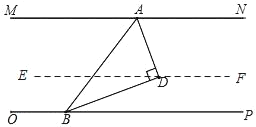
【题目】如图,MN∥OP,点A为直线MN上一定点,B为直线OP上的动点,在直线MN与OP之间且在线段AB的右方作点D,使得AD⊥BD.设∠DAB=α(α为锐角).
(1)求∠NAD与∠PBD的和;(提示过点D作EF∥MN)
(2)当点B在直线OP上运动时,试说明∠OBD﹣∠NAD=90°;
(3)当点B在直线OP上运动的过程中,若AD平分∠NAB,AB也恰好平分∠OBD,请求出此时α的值

【答案】(1)∠NAD+∠PBD=90°;(2)∠OBD﹣∠NAD=90°;(3)α=30°.
【解析】
(1)过点D作EF∥MN,则∠NAD=∠ADE,EF∥OP,依据平行线的性质可得到∠PBD=∠BDE,则∠NAD+∠PBD=∠ADB,最后,依据垂线的定义求解即可;
(2)由(1)得∠NAD=90°-∠PBD,然后结合∠OBD+∠PBD=180°,进行证明即可;
(3)先求得∠OBD的度数(用含α的式子表示),然后再利用(2)中的结论列方程求解即可.
(1)如图,过点D作EF∥MN,则∠NAD=∠ADE.
∵MN∥OP,EF∥MN,
∴EF∥OP.
∴∠PBD=∠BDE,
∴∠NAD+∠PBD=∠ADE+∠BDE=∠ADB.
∵AD⊥BD,
∴∠ADB=90°,
∴∠NAD+∠PBD=90°.
(2)由(1)得:∠NAD+∠PBD=90°,则∠NAD=90°﹣∠PBD.
∵∠OBD+∠PBD=180°,
∴∠OBD=180°﹣∠PBD,
∴∠OBD﹣∠NAD=(180°﹣∠PBD)﹣(90°﹣∠PBD)=90°.
(3)若AD平分∠NAB,AB也恰好平分∠OBD,则有∠NAD=∠BAD=α,∠NAB=2∠BAD=2α,∠OBD=2∠OBA.
∵OP∥MN,
∴∠OBA=∠NAB=2α,
∴∠OBD=4α.
由(2)知:∠OBD﹣∠NAD=90°,则4α﹣α=90°,解得:α=30°.


科目:初中数学 来源: 题型:
【题目】如图,将一个三角板放在边长为1的正方形![]() 上,并使它的直角顶点
上,并使它的直角顶点![]() 在对角线
在对角线![]() 上滑动,直角的一边始终经过点
上滑动,直角的一边始终经过点![]() ,另一边与射线
,另一边与射线![]() 相交于点
相交于点![]() .
.

(1)当点![]() 在
在![]() 边上时,过点
边上时,过点![]() 作
作![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,证明:
,证明:![]() ;
;
(2)当点![]() 在线段
在线段![]() 的延长线上时,设
的延长线上时,设![]() 、
、![]() 两点间的距离为
两点间的距离为![]() ,
,![]() 的长为
的长为![]() .
.
①直接写出![]() 与
与![]() 之间的函数关系,并写出函数自变量
之间的函数关系,并写出函数自变量![]() 的取值范围;
的取值范围;
②![]() 能否为等腰三角形?如果能,直接写出相应的
能否为等腰三角形?如果能,直接写出相应的![]() 值;如果不能,说明理由.
值;如果不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,![]() 中,
中,![]() ,求证:
,求证:![]() ;
;
(2)如图2,![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,垂足分别为
,垂足分别为![]() 、
、![]() ,
,![]() 与
与![]() 交于点
交于点![]() .试探究线段
.试探究线段![]() 与线段
与线段![]() 的数量关系.
的数量关系.
(3)如图3,![]() 中,
中,![]() ,
,![]() ,垂足为
,垂足为![]() ,若线段
,若线段![]() ,则
,则![]() 的面积为 .
的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
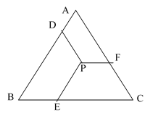
【题目】如图,已知等边△ABC的边长为10,P是△ABC内一点,PD平行AC,PE平行AD,PF平行BC,点D,E,F分别在AB,BC,AC上,则PD+PE+PF= _______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是BC上的中线,点E在线段AC上且EC=2AE,线段AD与线段BE交于点F,若△ABC对面积为3,则四边形EFDC的面积为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(a,0),C(b,2),且满足(a+b)2+|a-b+4|=0,过点C作CB⊥x轴于B.
(1)如图1,求△ABC的面积.
(2)如图2,若过B作BD∥AC交y轴于D,在△ABC内有一点E,连接AE.DE,若∠CAE+∠BDE=∠EAO+∠EDO,求∠AED的度数.
(3)如图3,在(2)的条件下,DE与x轴交于点M,AC与y轴交于点F,作△AME的角平分线MP,在PE上有一点Q,连接QM,∠EAM+2∠PMQ=45°,当AE=2AM,FO=2QM时,求点E的纵坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学将一张圆桌紧靠在矩形屋子的一角,与相邻两面墙相切,她把切点记为A、B,然后,她又在桌子边缘上任取一点P(异于A、B),则∠APB的度数为( )
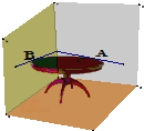
A. 45° B. 135° C. 45°或135° D. 90°或135°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售樱桃,已知樱桃的进价为15元/千克,如果售价为20元/千克,那么每天可售出250千克,如果售价为25元/千克,那么每天可获利2000元,经调查发现:每天的销售量y(千克)与售价x(元/千克)之间存在一次函数关系.
(1)求y与x之间的函数关系式;
(2)若樱桃的售价不得高于28元/千克,请问售价定为多少时,该超市每天销售樱桃所获的利润最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com