
����Ŀ����ͼ����һ�����ǰ���ڱ߳�Ϊ1��������![]() �ϣ���ʹ����ֱ�Ƕ���
�ϣ���ʹ����ֱ�Ƕ���![]() �ڶԽ���
�ڶԽ���![]() �ϻ�����ֱ�ǵ�һ��ʼ�վ�����
�ϻ�����ֱ�ǵ�һ��ʼ�վ�����![]() ����һ��������
����һ��������![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��

��1������![]() ��
��![]() ����ʱ������
����ʱ������![]() ��
��![]() �ֱ�
�ֱ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() ��֤����
��֤����![]() ��
��
��2������![]() ���߶�
���߶�![]() ���ӳ�����ʱ����
���ӳ�����ʱ����![]() ��
��![]() �����ľ���Ϊ
�����ľ���Ϊ![]() ��
��![]() �ij�Ϊ
�ij�Ϊ![]() ��
��
��ֱ��д��![]() ��
��![]() ֮��ĺ�����ϵ����д�������Ա���
֮��ĺ�����ϵ����д�������Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��![]() �ܷ�Ϊ���������Σ�����ܣ�ֱ��д����Ӧ��
�ܷ�Ϊ���������Σ�����ܣ�ֱ��д����Ӧ��![]() ֵ��������ܣ�˵�����ɣ�
ֵ��������ܣ�˵�����ɣ�
���𰸡���1������������2���� ����
����![]() ������������
������������![]() ��
��
��������
��1�����������ε�����֤��![]() ��������⣻
��������⣻
��2���ٸ���������ͼ���������ε����ʿ�֪��![]() ʱ����
ʱ����![]() ���߶�
���߶�![]() ���ӳ����ϣ�ͬ���ɵ�
���ӳ����ϣ�ͬ���ɵ�![]() ���õ�MP=NQ�����õ���ֱ�������ε����ʿ�֪MP=
���õ�MP=NQ�����õ���ֱ�������ε����ʿ�֪MP=![]() x��NC=CD-DN=1-
x��NC=CD-DN=1-![]() x��CQ=y������MP=NQ������⣻
x��CQ=y������MP=NQ������⣻
����![]() �ǵ��������Σ���PCQ=135����CP=CQ����������ⷽ�̼������ ��
�ǵ��������Σ���PCQ=135����CP=CQ����������ⷽ�̼������ ��
��1��֤��������������![]() �У�
�У�![]() Ϊ�Խ��ߣ�
Ϊ�Խ��ߣ�
��![]() ��
��![]() ����
����![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
����![]() ��
��
��![]() ��
��
��![]() ����
����![]() ��
��
����![]() ����
����![]() ��
��
��![]() ��
��
��![]() ��
�У�
��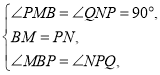
��![]() ����
����![]() ��
��
��2������ͼ����![]() ���߶�
���߶�![]() ���ӳ����ϣ�
���ӳ����ϣ�
ͬ��1����֤![]() ��
��
��MP=NQ��
�ڵ���ֱ��������AMP�У�AP=![]() =x
=x
��MP=![]() x=AM,
x=AM,
��NC=BM=AB-AM=1-![]() x
x
��NQ=NC+CQ=1-![]() x+y
x+y
��![]() x=1-
x=1-![]() x+y
x+y
�����![]()
��P��λ��AC�е�ʱ��Q��ǡ����C�㣬��AP��AC=![]()
��![]()
��![]() ��
��![]() ֮��ĺ�����ϵ��
֮��ĺ�����ϵ��![]() ��
��![]() ��
��
����![]() ʱ��
ʱ��![]() ��Ϊ���������Σ�
������������
���ɣ�����![]() ��
��![]() ���ӳ����ϣ�CQ=
���ӳ����ϣ�CQ=![]() ��CQ=AC-AP=
��CQ=AC-AP=![]() ��
��
��![]() �ǵ��������Σ���PCQ=��PCB+��BCQ=45��+90��=135����
�ǵ��������Σ���PCQ=��PCB+��BCQ=45��+90��=135����
��CP=CQ������
��![]() ʱ�����
ʱ�����![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
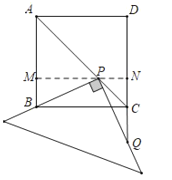
����Ŀ����ͼ����һ��ľ��������ı���Ϳ����ɫ��Ȼ�������ηָ��27����С��ͬ��С�����壬����ЩС������������ȡ��һ������ȡ����С�����壻
��1��ֻ��һ��Ϳ����ɫ�ĸ��ʣ�
��2������������Ϳ����ɫ�ĸ��ʣ�
��3�������涼û����ɫ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ����Ӧ��ί������������ɫ���������ܼ������ĺ��٣��Ҹ��̳���3300Ԫ�����ס������ֽ��ܵƹ���100ֻ���ܿ����꣮�����ֽ��ܵƵĽ��ۡ��ۼ����±���
���ۣ�Ԫ/ֻ�� | �ۼۣ�Ԫ/ֻ�� | |
���ֽ��ܵ� | 30 | 40 |
���ֽ��ܵ� | 35 | 50 |
��1�����Ҹ��̳��ס������ֽ��ܵƸ������˶���ֻ��
��2��ȫ������100ֻ���ܵƺ��̳����ƻ�������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ��ȤС���У�С��������ѧ̽��������߳�Ϊ![]() ��������ABCD��߳�Ϊ
��������ABCD��߳�Ϊ![]() ��������AEFG��ͼ1λ�÷��ã�AD��AE��ͬһ��ֱ���ϣ�AB��AG��ͬһ��ֱ����.
��������AEFG��ͼ1λ�÷��ã�AD��AE��ͬһ��ֱ���ϣ�AB��AG��ͬһ��ֱ����.
(1)С������DG��BE���������˵������.
(2)��ͼ2��С����������ABCD�Ƶ�A��ʱ����ת������Bǡ�������߶�DG��ʱ��������������ʱBE�ij�.


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ڼ䣬��λ�ҳ��ƻ�����������ѧ��ȥ���Σ�������ϵ�˱��۾�Ϊÿ��1000Ԫ�����������磮��Э�̣�����������Ż������ǣ���λ�ҳ�ȫ���շѣ�ѧ������7���շѣ�����������Ż������ǣ�ѧ�����ҳ�����8���շѣ���������λ�ҳ�����x��ѧ��ȥ���У��ס�����������շѷֱ�Ϊy����y����
��1��д��y����y����x�ĺ�����ϵʽ��
��2��ѧ��������ʲô����£�ѡ���ĸ���������㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ��
��![]() ����
����![]() �Ķ���.
�Ķ���.

��1����գ��ڿհ״����Ͻ����������.
�⣺����![]() ��
��![]() ������ͼ��
������ͼ��
��![]() ___________�㣬 �� ��
___________�㣬 �� ��
����Ϊ![]() ������֪��
������֪��
����![]() ___________��.
___________��.
��Ϊ![]() ��
��
����![]() �� �� ��
�� �� ��
����Ϊ![]() ������֪��
������֪��
����![]() ___________�㣬
___________�㣬
����![]() ___________��.
___________��.
��2��������һ�ֽⷨ��![]() �Ķ���.
�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
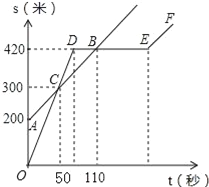
����Ŀ��ij��ѧ��С��������ʦһ��һ����ֱ���ܵ��϶������壬��������С������һ���������ʦ���ܣ���С������ʱ������ʦ�Ѿ������200���ˣ����Ǿ����ľ���s���ף���С��������ʱ��t���룩֮��Ĺ�ϵ��ͼ��ʾ����������������ͼ�и�������Ϣ������������⣺
��1���������仯�����У��Ա������� ������������� ����
��2������ʦ���ٶ�Ϊ�� ����/�룻С�����ٶ�Ϊ�� ����/�룻
��3��С��������ʦ������ ���Σ�����ʱ�����ľ���ֱ�Ϊ�� ���ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʻ�е�����ײ������ʱ���������̶�ͨ���á�ײ��Ӱ�족��������������ײ��Ӱ��I������������ʻ�ٶ�v(km/min)����ʾ���±���ij���ͺ���������ʻ�ٶ���ײ��Ӱ����������ݣ�
v(km/min) | 0 | 1 | 2 | 3 | 4 |
I | 0 | 2 | 8 | 18 | 32 |
(1)������ϱ��е���������ֱ������ϵ���������(v��I)����Ӧ�ĵ㣬���ù⻬���߽���������������

(2)��д�±��������ݱ������ݵij��ֹ�����������v��ʾI�Ķ��κ�������ʽ��
v(km/min) | 1 | 2 | 3 | 4 |
|
|
|
|
|
(3)���������ٶȷֱ���1.5 km/min��2.5 km/min��4.5 km/minʱ��������õ���ײ��Ӱ�칫ʽ������ײ��Ӱ��ֱ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��MN��OP����AΪֱ��MN��һ���㣬BΪֱ��OP�ϵĶ��㣬��ֱ��MN��OP֮�������߶�AB���ҷ�����D��ʹ��AD��BD�����DAB����(��Ϊ���)��
(1)���NAD���PBD�ĺͣ�(��ʾ����D��EF��MN)
(2)����B��ֱ��OP���˶�ʱ����˵����OBD����NAD��90�㣻
(3)����B��ֱ��OP���˶��Ĺ����У���ADƽ�֡�NAB��ABҲǡ��ƽ�֡�OBD���������ʱ����ֵ

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com