
【题目】在平面直角坐标系中,已知抛物线经过A(﹣4,0),B(0,﹣4),C(2,0)三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,△AMB的面积为S.求S关于m的函数关系式,并求出S的最大值.
【答案】
(1)
解:设抛物线解析式为y=a(x+4)(x﹣2),
将B(0,﹣4)代入得:﹣4=﹣8a,即a= ![]() ,
,
则抛物线解析式为y= ![]() (x+4)(x﹣2)=
(x+4)(x﹣2)= ![]() x2+x﹣4;
x2+x﹣4;
(2)
解:过M作MN⊥x轴,

将x=m代入抛物线得:y= ![]() m2+m﹣4,即M(m,
m2+m﹣4,即M(m, ![]() m2+m﹣4),
m2+m﹣4),
∴MN=| ![]() m2+m﹣4|=﹣
m2+m﹣4|=﹣ ![]() m2﹣m+4,ON=﹣m,
m2﹣m+4,ON=﹣m,
∵A(﹣4,0),B(0,﹣4),∴OA=OB=4,
∴△AMB的面积为S=S△AMN+S梯形MNOB﹣S△AOB
= ![]() ×(4+m)×(﹣
×(4+m)×(﹣ ![]() m2﹣m+4)+
m2﹣m+4)+ ![]() ×(﹣m)×(﹣
×(﹣m)×(﹣ ![]() m2﹣m+4+4)﹣
m2﹣m+4+4)﹣ ![]() ×4×4
×4×4
=2(﹣ ![]() m2﹣m+4)﹣2m﹣8
m2﹣m+4)﹣2m﹣8
=﹣m2﹣4m
=﹣(m+2)2+4,
当m=﹣2时,S取得最大值,最大值为4.
【解析】(1)根据抛物线与x轴的交点A与C坐标设出抛物线的二根式方程,将B坐标代入即可确定出解析式;(2)过M作x轴垂线MN,三角形AMB面积=梯形MNOB面积+三角形AMN面积﹣三角形AOB面积,求出即可.


科目:初中数学 来源: 题型:
【题目】如图,二次函数y=x2﹣4x的图象与x轴、直线y=x的一个交点分别为点A,B,CD是线段OB上的一动线段,且CD=2,过点C,D的两直线都平行于y轴,与抛物线相交于点F,E,连接EF. 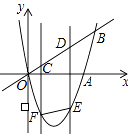
(1)点A的坐标为 , 线段OB的长=;
(2)设点C的横坐标为m ①当四边形CDEF是平行四边形时,求m的值;
②连接AC、AD,求m为何值时,△ACD的周长最小,并求出这个最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:等腰三角形、平行四边形、菱形、双曲线、抛物线.这些都是我们在初中学习阶段学过的几何图形或函数的图象,那么从它们之中随机抽取两个,得到的都是中心对称图形的概率是( )
A.![]()
B.![]()
C.![]()
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠A=90° 
(1)请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切(保留作图痕迹,不写作法和证明).
(2)若∠B=60°,AB=3,求⊙P的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C是圆O上的三点,且四边形ABCO是平行四边形,OF⊥OC交圆O于点F,则∠BAF等于( ) 
A.12.5°
B.15°
C.20°
D.22.5°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下是一位同学所做的实数运算解题过程的一部分. ﹣ ![]() ﹣|﹣1|2017﹣(π﹣3.14)0+4cos60°
﹣|﹣1|2017﹣(π﹣3.14)0+4cos60°
=﹣ ![]() +1﹣1+4×
+1﹣1+4× ![]() .
.
(1)指出上面解答过程中的错误,并写出正确的解答过程;
(2)若分式方程 ![]() +1=
+1= ![]() 的解与(1)中的最终结果相同,求a的值.
的解与(1)中的最终结果相同,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com