
【题目】已知关于x、y的方程组 ![]() ,给出下列结论: ①
,给出下列结论: ① ![]() 是方程组的解;
是方程组的解;
②无论a取何值,x,y的值都不可能互为相反数;
③当a=1时,方程组的解也是方程x+y=4﹣a的解;
④x,y的都为自然数的解有4对.
其中正确的个数为( )
A.1个
B.2个
C.3个
D.4个
【答案】C
【解析】解:①将x=5,y=﹣1代入方程组得: ![]() , 由①得a=2,由②得a=
, 由①得a=2,由②得a= ![]() ,故①不正确.
,故①不正确.
②解方程 ![]()
①﹣②得:8y=4﹣4a
解得:y= ![]()
将y的值代入①得:x= ![]() ,
,
所以x+y=3,故无论a取何值,x、y的值都不可能互为相反数,故②正确.
③将a=1代入方程组得: ![]()
解此方程得: ![]()
将x=3,y=0代入方程x+y=3,方程左边=3=右边,是方程的解,故③正确.
④因为x+y=3,所以x、y都为自然数的解有 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,.故④正确.
,.故④正确.
则正确的选项有②③④,
故选:C.
【考点精析】本题主要考查了二元一次方程组的解的相关知识点,需要掌握二元一次方程组中各个方程的公共解,叫做这个二元一次方程的解才能正确解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】计算:
(1)(﹣2)2015×(﹣ ![]() )2014
)2014
(2)2x3(﹣3x)2÷(﹣x)
(3)(6m2n﹣6m2n2﹣3m2)÷(﹣3m2)
(4)(﹣1)100﹣(3+π)0﹣(﹣ ![]() )﹣2 .
)﹣2 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校欲招聘一名数学教师,学校对甲、乙、丙三位候选人进行了三项能力测试,各项测试成绩满分均为100分,根据结果择优录用.三位候选人的各项测试成绩如下表所示:
测试项目 | |||
测试成绩/分 | |||
甲 | 乙 | 丙 | |
教学能力 | 85 | 73 | 73 |
科研能力 | 70 | 71 | 65 |
组织能力 | 64 | 72 | 84 |
(1)如果根据三项测试的平均成绩,谁将被录用,说明理由;
(2)根据实际需要,学校将教学、科研和组织三项能力测试得分按5∶3∶2的比例确定每人的成绩,谁将被录用,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,点C为半径OB上一点,过点C作CD丄AB交半圆O于点D,将△ACD沿AD折叠得到△AED,AE交半圆于点F,连接DF.
(1)求证:DE是半圆的切线:
(2)连接0D,当OC=BC时,判断四边形ODFA的形状,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数:
每人加工零件个数 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件数的平均数、中位数和众数.
(2)假如生产部负责人把每位工人的月加工零件个数定为260,你认为这个定额是否合理?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市招聘教师,对应聘者分别进行教学能力、科研能力、组织能力三项测试,其中甲、乙两人的成绩如下表:(单位:分)

(1)根据实际需要,将教学能力、科研能力、组织能力三项测试得分按5∶3∶2的比确定最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
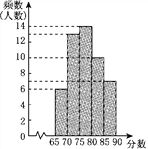
(2)按照(1)中的成绩计算方法,将每位应聘者的最后成绩绘制成如图所示的频数分布直方图(每组分数段均包含左端数值,不包含右端数值),并决定由高分到低分录用8人.甲、乙两人能否被录用?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明解方程![]() 的过程如下.请指出他解答过程中的错误,并写出正确的解答过程.
的过程如下.请指出他解答过程中的错误,并写出正确的解答过程.
解:方程两边同乘x,得1-(x-2)=1.……①
去括号,得1-x-2=1.……②
合并同类项,得-x-1=1.……③
移项,得-x=2.……④
解得x=-2.……⑤
∴原方程的解为x=-2.……⑥
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com