Question

【题目】如图1，在正方形ABCD中，P是对角线BD上的一点，点E在AD的延长线上，且PA=PE，PE交CD于F．
（1）证明：PC=PE；
（2）求∠CPE的度数；
（3）如图2，把正方形ABCD改为菱形ABCD，其他条件不变，当∠ABC=116°时，则∠EPC= ．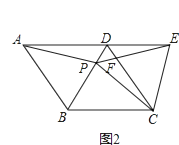

Answer 1

【答案】
（1）证明：∵四边形ABCD为正方形，

∴BA=BC，∠ABD=∠CBD=45°，

在△ABP和△CBP中

，

∴△ABP≌△CBP，

∴PA=PC，

∵PA=PE，

∴PC=PE；

（2）解：∵△ABP≌△CBP，

∴∠PAB=∠PCB，

∴∠PAD=∠PCD，

∵PA=PE，

∴∠PAE=∠E，

∴∠PCD=∠E，

而∠DFE=∠PFC，

∴∠CPF=∠EDF=90°，

（3）64°
【解析】（3）∵四边形ABCD为菱形，

∴BA=BC，∠ABD=∠CBD=58°，∠ADC=∠ABC=116°，

∴∠EDC=64°，

在△ABP和△CBP中

，

∴△ABP≌△CBP，

∴PA=PC，∠PAB=∠PCB，

∴∠PAD=∠PCP，

∵PA=PE，

∴∠PAD=∠PEA，

∴∠PCD=∠PED

而∠DFE=∠PFC，

∴∠CPF=∠EDF=64°．

所以答案是64°．

【考点精析】通过灵活运用菱形的性质和正方形的性质，掌握菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半；正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题．