
【题目】某超市为了答谢顾客,凡在本超市购物的顾客,均可凭购物小票参与抽奖活动,奖品是三种瓶装饮料,它们分别是:绿茶、红茶和可乐,抽奖规则如下:①如图是一个材质均匀可自由转动的转盘,转盘被等分成五个扇形区域,每个区域上分别写有“可”、“绿”、“乐”、“茶”、“红”字样;②参与一次抽奖活动的顾客可进行两次“有效随机转动”(当转动转盘,转盘停止后,可获得指针所指区域的字样,我们称这次转动为一次“有效随机转动”);③假设顾客转动转盘,转盘停止后,指针指向两区域的边界,顾客可以再转动转盘,直到转动为一次“有效随机转动”;④当顾客完成一次抽奖活动后,记下两次指针所指区域的两个字,只要这两个字的组合和奖品名称相同(与字的顺序无关),便可获得相应奖品一瓶;不相同时,不能获得任何奖品.
根据以上规则,回答下列问题:

(1)求一次“有效随机转动”可获得“乐”字的概率.
(2)有一名顾客凭本超市的购物小票,参与了一次抽奖活动,请你用列表或画树状图的方法,求该顾客经过两次“有效随机转动”后,获得一瓶可乐的概率.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)由转盘被等分成五个扇形区域,每个区域上分别写有“可”、“绿”、“乐”、“茶”、“红”字样;直接利用概率公式求解即可求得答案;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与该顾客经过两次“有效随机转动”后,获得一瓶可乐的情况,再利用概率公式求解即可求得答案.
试题解析:(1)∵转盘被等分成五个扇形区域,每个区域上分别写有“可”、“绿”、“乐”、“茶”、“红”字样;∴一次“有效随机转动”可获得“乐”字的概率为: ![]() ;
;
(2)画树状图得:
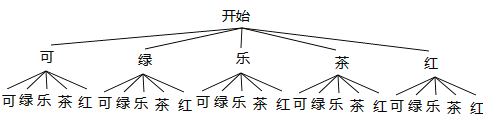
∵共有25种等可能的结果,该顾客经过两次“有效随机转动”后,获得一瓶可乐的有2种情况,∴该顾客经过两次“有效随机转动”后,获得一瓶可乐的概率为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示,在数轴上A点表示数a,B点表示数b,且a、b满足|2a+6|+|b﹣9|=0
(1)点A表示的数为 ,点B表示的数为 ;
(2)若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,请在点A、点B之间的数轴上找一点C,使BC=2AC,则C点表示的数为 ;
(3)在(2)的条件下,若一动点P从点A出发,以3个单位长度/秒速度由A向B运动;同一时刻,另一动点Q从点C出发,以1个单位长度/秒速度由C向B运动,终点都为B点.当一点到达终点时,这点就停止运动,而另一点则继续运动,直至两点都到达终点时才结束整个运动过程.设点Q运动时间为t秒.
请用含t的代数式表示:点P到点A的距离PA= ,点Q到点B的距离QB= ;点P与点Q之间的距离 PQ= .
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市长途客运站每天6:30—7:30开往某县的三辆班车票价相同,但车的舒适程度不同.小张和小王因事需在这一时段乘车去该县,但不知道三辆车开来的顺序,两人采用不同的乘车方案:小张无论如何决定乘坐开来的第一辆车,而小王则是先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适状况.若第二辆车的状况比第一辆车好,他就上第二辆车;若第二辆车不如第一辆车,他就上第三辆车.若按这三辆车的舒适程度分为优、中、差三等,请你思考并回答下列问题:
(1)三辆车按出现的先后顺序共有哪几种可能?
(2)请列表分析哪种方案乘坐优等车的可能性大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
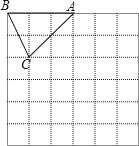
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,△ABC的顶点A、B、C在小正方形的顶点上,将△ABC向下平移4个单位、再向右平移3个单位得到△A1B1C1
(1)在网格中画出△A1B1C1;
(2)计算线段AC在变换到A1C1的过程中扫过区域的面积(重叠部分不重复计算).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活的情况进行调查统计,并绘制了如图所示的统计图,根据统计图提供的信息解决下列问题:
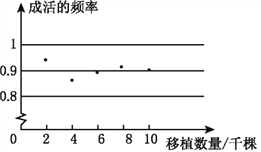
(1)这种树苗成活的频率稳定在___________,成活的概率估计值为___________.
(2)该地区已经移植这种树苗5万棵.
①估计这种树苗成活___________万棵.
②如果该地区计划成活18万棵这种树苗,那么还需移植这种树苗约多少万棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,P是对角线BD上的一点,点E在AD的延长线上,且PA=PE,PE交CD于F. 
(1)证明:PC=PE;
(2)求∠CPE的度数;
(3)如图2,把正方形ABCD改为菱形ABCD,其他条件不变,当∠ABC=116°时,则∠EPC= . 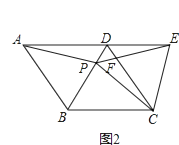
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,推理填空:

(1)∵∠1=_______(已知),
∴AC∥ED(同位角相等,两直线平行).
(2)∵∠2=______(已知),
∴AB∥FD(内错角相等,两直线平行).
(3)∵∠2+_______=180°(已知),
∴AC∥ED(同旁内角互补,两直线平行).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com