
【题目】已知关于x的一元二次方程x2﹣2x+m+2=0有两个不等的实数根x1和x2
(1)求m的取值范围并证明x1x2=m+2;
(2)若|x1﹣x2|=2,求m的值.
【答案】解:(1)∵关于x的一元二次方程x2﹣2x+m+2=0有两个不等的实数根x1和x2 ,
所以△=(﹣2)2﹣4(m+2)=﹣4m﹣4>0
解得m<﹣1,
根据求根公式![]() ,
,![]()
∴![]() ;
;
(2)根据根与系数的关系得x1+x2=2,x1x2=m+2,
∵|x1﹣x2|=2,
∴(x1﹣x2)2=4,
∴(x1+x2)2﹣4x1x2=4,
∴4﹣4(m+2)=4,
解得m=﹣2.
【解析】(1)根据判别式的意义得到△=(﹣2)2﹣4(m+2)=﹣4m﹣4>0解得m<﹣1,再利用求根公式解方程,然后计算x1x2;
(2)先根据根与系数的关系得x1+x2=2,x1x2=m+2,再把|x1﹣x2|=2两边平方得到(x1﹣x2)2=4,接着利用完全平方公式变形得到(x1+x2)2﹣4x1x2=4,所以4﹣4(m+2)=4,
然后解关于m的方程即可.
【考点精析】解答此题的关键在于理解求根公式的相关知识,掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根,以及对根与系数的关系的理解,了解一元二次方程ax2+bx+c=0(a≠0)的根由方程的系数a、b、c而定;两根之和等于方程的一次项系数除以二次项系数所得的商的相反数;两根之积等于常数项除以二次项系数所得的商.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
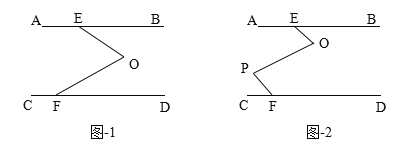
【题目】如图1,AB∥CD,EOF是直线AB、CD间的一条折线.
(1)说明:∠O=∠BEO+∠DFO.
(2)如果将折一次改为折二次,如图-2,则∠BEO、∠O、∠P、∠PFC会满足怎样的关系,证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】服装厂准备生产某种样式的服装40000套,分黑色和彩色两种.
(1)若生产黑色服装的套数不多于彩色服装套数的![]() , 问最多生产多少套黑色服装?
, 问最多生产多少套黑色服装?
(2)目前工厂有100名工人,平均每人生产400套,由于展品会上此种样式服装大受欢迎,工厂计划增加产量;由于条件发生变化,人均生产套数将减少1.25a%(20<a<30),要使生产总量增加10%,则工人需增加2.4a%,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定一种新的运算:a★b=a×b﹣a﹣b2+1,例如3★(﹣4)=3×(﹣4)﹣3﹣(﹣4)2+1. 请计算下列各式的值①2★5 ②(﹣2)★(﹣5).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com