Question

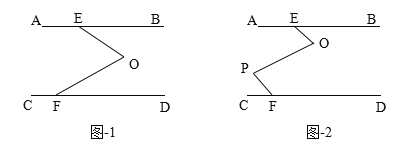
【题目】如图1，AB∥CD，EOF是直线AB、CD间的一条折线.

（1）说明：∠O=∠BEO+∠DFO.

（2）如果将折一次改为折二次，如图-2，则∠BEO、∠O、∠P、∠PFC会满足怎样的关系，证明你的结论.

Answer 1

【答案】证明见解析

【解析】试题分析：（1）过O作OM∥AB，根据平行线性质推出∠BEO=∠MOE，∠DFO=∠MOF，相加即可求出答案；

（2）过O作OM∥AB，PN∥AB，根据平行线性质求出∠BEO=∠EOM，∠PFC=∠NPF，∠MOP=∠NPO，代入求出即可．

试题解析：（1）证明：过O作OM∥AB，∵AB∥CD，∴AB∥OM∥CD，∴∠BEO=∠MOE，∠DFO=∠MOF，∴∠BEO+∠DFO=∠EOM+∠FOM，即∠EOF=∠BEO+∠DFO．

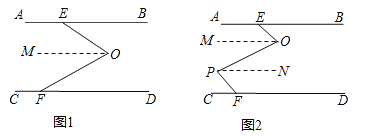
（2）∠BEO+∠P=∠O+∠PFC．证明如下：

过O作OM∥AB，PN∥AB，∵AB∥CD，∴AB∥OM∥PN∥CD，∴∠BEO=∠EOM，∠PFC=∠NPF，∠MOP=∠NPO，∴∠EOP﹣∠OPF=（∠EOM+∠MOP）﹣（∠OPN+∠NPF）=∠EOM﹣∠NPF，∠BEO﹣∠PFC=∠EOM﹣∠NPF，∴∠BEO﹣∠PFC=∠EOP﹣∠OPF，∴∠BEO+∠OPF=∠EOP+∠PFC．