
����Ŀ����ƽ��ֱ������ϵ![]() �У�������
��������![]() ��
��
��1��������������ֱ��![]() ����A��B���㣬��B��y���ϣ���������ߵı���ʽ����A�����ꣻ
����A��B���㣬��B��y���ϣ���������ߵı���ʽ����A�����ꣻ
��2��������Ϊ�����ĵ��Ϊ�����㣮
�ٽ���1���е���������A��B����֮��IJ��ּ���![]() ������A��B���㣩��ֱ��д��
������A��B���㣩��ֱ��д��![]() �ϵĺ���������ꣻ
�ϵĺ���������ꣻ
��������![]() ��ֱ��
��ֱ��![]() ����C��D���㣬����������C��D����֮��IJ��ּ���
����C��D���㣬����������C��D����֮��IJ��ּ���![]() ������C��D���㣩����
������C��D���㣩����![]() ��ǡ�����������㣬��Ϻ�����ͼ����m��ȡֵ��Χ��
��ǡ�����������㣬��Ϻ�����ͼ����m��ȡֵ��Χ��
���𰸡���1��![]() ��A����Ϊ��-4��2������2���٣�-3��-1������-2��-2������-1��-1����
��A����Ϊ��-4��2������2���٣�-3��-1������-2��-2������-1��-1����
��![]() ��
��![]() .
.
��������
��1���������⣬��B����Ϊ��0��2������B���������![]() ��������⣻
��������⣻
��2���ٰ�x=-3��x=-2��x=-1������![]() �����ɣ�
�����ɣ�
������![]() ��
��![]() ���ã�
���ã�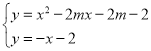 ����C��D������ֱ��ǣ���-1��-1������2m��-2m-2�������������m�ķ�Χ.
����C��D������ֱ��ǣ���-1��-1������2m��-2m-2�������������m�ķ�Χ.
��1������������ֱ��![]() ����A��B���㣬��B��y���ϣ�
����A��B���㣬��B��y���ϣ�
��B������0��2����
��B��0��2������![]() ���ã�
���ã�![]() ����ã�m=-2��
����ã�m=-2��
�������ߵý���ʽΪ��![]() ��
��
��y=2ʱ��![]() ����ã�
����ã�![]() ��
��
��A������-4��2����
��2���١�A����Ϊ��-4��2����B����Ϊ��0��2����
�൱x=-3ʱ��![]() ��
��
��x=-2ʱ��![]() ��
��
��x=-1ʱ��![]() ��
��
![]() �ϵĺ�����������ǣ���-3��-1������-2��-2������-1��-1��
�ϵĺ�����������ǣ���-3��-1������-2��-2������-1��-1��
������![]() ��
��![]() ���ã�
���ã�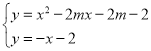 ��
��
��![]() ������
������![]() ��
��
��![]() ����ã�
����ã�![]() ��
��
��C��D������ֱ��ǣ���-1��-1������2m��-2m-2����
��![]() ��ǡ�����������㣬
��ǡ�����������㣬
������������ĺ�����Ϊ��x=0��x=1��x=-2��x=-3��
��![]() ��
��![]()
��![]() ��
��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCD�У�BC��10cm��DC��6cm����E��F�ֱ�Ϊ��AB��BC�ϵ��������㣬E�ӵ�A������ÿ��5cm���ٶ���B�˶���F�ӵ�B������ÿ��3cm���ٶ���C�˶������˶�ʱ��Ϊt�룮����AFD����AED����t��ֵ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=-x2+bx+c�Ķ���ΪC���Գ���Ϊֱ��x=1���Ҿ�����A��3��-1������y�ύ�ڵ�B��
��1���������ߵĽ���ʽ��
��2���ж���ABC����״����˵�����ɣ�
��3��������A��ֱ�߽��������ڵ�P����x���ڵ�Q����S��OPA=2S��OQA���������P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() ��ͼ��ԭ�㣬�������ϣ��Գ���Ϊֱ��
��ͼ��ԭ�㣬�������ϣ��Գ���Ϊֱ��![]() �����������������ۣ���mΪ����ʵ��������
�����������������ۣ���mΪ����ʵ��������![]() ���ڷ���
���ڷ���![]() ����������ȵ�ʵ������һ����С��0����һ��������2��˵����ȷ���ǣ� ��
����������ȵ�ʵ������һ����С��0����һ��������2��˵����ȷ���ǣ� ��
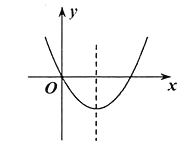
A.�ٶԣ��ڴ�B.�ٴ����ڶ�C.�٢ڶ���D.�٢ڶ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������![]() �У���E�ڱ�
�У���E�ڱ�![]() �ϣ�����E�Ƶ�D��ʱ����ת�õ���F������Fǡ�����ڱ�
�ϣ�����E�Ƶ�D��ʱ����ת�õ���F������Fǡ�����ڱ�![]() ���ӳ����ϣ�����
���ӳ����ϣ�����![]() ��
��![]() ��
��![]() ��
��
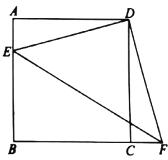
��1���ж�![]() ����״����˵�����ɣ�
����״����˵�����ɣ�
��2����![]() ����
����![]() �����Ϊ________��
�����Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�ǵȱ������Σ���ABΪֱ������O����BC���ڵ�D����AC���ڵ�F����DE��AC�ڵ�E��
��1����֤��DE����O�����ߣ�
��2������ABC�ı߳�Ϊ4����EF�ij��ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������M1��y����x2+4x��x�������ڵ�A����������M1������ƽ��3����λ��������ƽ��3����λ�õ�������M2��M1��M2���ڵ�B��ֱ��OB��M2�ڵ�C��
��1����������M2�Ľ���ʽ��
��2����P��������M1��AB���һ�㣬��PQ��x�ύ������M2�ڵ�Q������CP��CQ�����P�ĺ�����Ϊm����mΪ��ֵʱ��ʹ��CPQ��������������ֵ��
��3����ͼ2����ֱ��OB����ƽ�ƣ���������M1�ڵ�E��F����������M2�ڵ�G��H����![]() ��ֵ�Ƿ�Ϊ��ֵ��֤����Ľ��ۣ�
��ֵ�Ƿ�Ϊ��ֵ��֤����Ľ��ۣ�
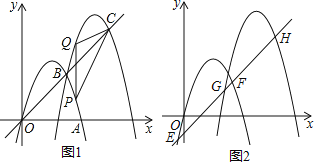
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ݱ�������2018��8��������������������������ֳ�������˲��ɹ�������ʧ��ij��ֳ��Ϊ��Ԥ������������������Ϯ��ÿ�����������ҩѬ��������֪һƿҩ���ͷŹ����У�һ��Ȧ����ÿ���������к�ҩ��y�����ˣ���ʱ��x�����ӣ�֮������������������ϵ��ҩ���ͷ����y��x֮�����㷴����������ϵ����ͼ��ʾ�����ͼ���ṩ����Ϣ�����������.
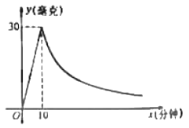
��1���ֱ���![]() ��
��![]() ʱ��y��x֮������ĺ�����ϵʽ��
ʱ��y��x֮������ĺ�����ϵʽ��
��2���ݲⶨ����������ÿ�����ĺ�ҩ��������6����ʱ����������Ч����ô���Ѭҩ����Ч����ʱ���Ƕ��ٷ��ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼһ�������ߣ�y=��x��x��3����0��x��3������ΪC1������x�ύ�ڵ�O��A1����C1��A1��ת180��õ�C2����x����A2����C2��A2��ת180��õ�C3����x����A3����˽�����ȥ��ֱ���õ�C10������P��28��m���ڵ�10��������C10�ϣ���m��ֵΪ��������

A. 1 B. ��1 C. 2 D. ��2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com