
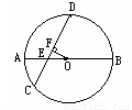
如图,⊙O的直径AB和弦CD相交于点E,已知AE=1cm,EB=5cm,∠DEB=600,求弦CD的长。
2 cm.
cm.
【解析】
试题分析:作OF⊥CD于F,连接OD,求出AB=6cm,半径OD=3cm,在Rt△OFE中,OE=2cm,∠OEF=60°,由勾股定理求出OF= cm,在Rt△OFD中,由勾股定理得求出FD=
cm,在Rt△OFD中,由勾股定理得求出FD= cm,由垂径定理得出DC=2DF,代入即可;
cm,由垂径定理得出DC=2DF,代入即可;
试题解析:作OF⊥CD于F,连接OD,

∵AE=1cm,BE=5cm,E在直径AB上,
∴AB=1cm+5cm=6cm,半径OD=3cm,
∵在Rt△OFE中,OE=3cm-1cm=2cm,∠OEF=60°,
∴OF= cm,
cm,
在Rt△OFD中,由勾股定理得:FD= cm,
cm,
∵OF⊥CD,
∴由垂径定理得:DC=2DF=2 cm.
cm.
考点:1.垂径定理;2.勾股定理.


科目:初中数学 来源:2013-2014学年浙江省宁波市九年级上学期第一次月考数学试卷(解析版) 题型:解答题
如图,已知一次函数 与反比例函数
与反比例函数 的图象交于A(2,4)、B(﹣4,n)两点.
的图象交于A(2,4)、B(﹣4,n)两点.

(1)分别求出 和
和 的解析式;
的解析式;
(2)求 =
= 时,x的值;
时,x的值;
(3)根据图象直接写出 >
> 时,x的取值范围.
时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省宁波市九年级上学期第一次月考数学试卷(解析版) 题型:选择题
如图,点B在反比例函数y=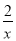 (x>0)的图象上,过点B分别向x轴,y轴作垂线,垂足分别为A,C,则矩形OABC的面积为( )
(x>0)的图象上,过点B分别向x轴,y轴作垂线,垂足分别为A,C,则矩形OABC的面积为( )

A、1 B、2 C、3 D、4
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省宁波市九年级上学期期中考试数学试卷(解析版) 题型:解答题
“绿色出行,低碳健身”已成为广大市民的共识.某旅游景点新增了一个公共自行车停车场,6:00至18:00市民可在此借用自行车,也可将在各停车场借用的自行车还于此地.林华同学统计了周六该停车场各时段的借、还自行车数,以及停车场整点时刻的自行车总数(称为存量)情况,表格中x=1时的y值表示7:00时的存量,x=2时的y值表示8:00时的存量…依此类推.他发现存量y(辆)与x(x为整数)满足如图所示的一个二次函数关系.

根据所给图表信息,解决下列问题:
(1)m= ,解释m的实际意义: ;
(2)求整点时刻的自行车存量y与x之间满足的二次函数关系式;
(3)已知9:00~10:O0这个时段的还车数比借车数的3倍少4,求此时段的借车数.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省宁波市九年级上学期期中考试数学试卷(解析版) 题型:填空题
将抛物线 的图象向右平移1个单位,再向上平移2个单位后,得到的新抛物线解析式是 .
的图象向右平移1个单位,再向上平移2个单位后,得到的新抛物线解析式是 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省宁波市九年级上学期期中考试数学试卷(解析版) 题型:选择题
已知⊙O半径为5,线段OP=6,A为OP的中点,点A与⊙O的位置关系是( )
A、点A在⊙O内 B、点A在⊙O上 C、点A在⊙O外 D、不能确定
查看答案和解析>>
科目:初中数学 来源:2013-2014学年浙江省丽水市莲都区九年级第一次中考模拟数学试卷(解析版) 题型:填空题
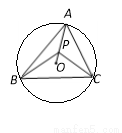
如图,⊙O是△ABC的外接圆,∠BAC=55°,点P在半径AO上(不与A,O重合),则∠BPC可能为 度(写出一个即可);
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省中考模拟数学试卷(解析版) 题型:解答题
如图,在△ABC中,AB=AC=10cm,BC=16cm,DE=4cm.动线段DE(端点D从点B开始)沿BC边以1cm/s的速度向点C运动,当端点E到达点C时运动停止.过点E作EF∥AC交AB于点F(当点E与点C重合时,EF与CA重合),连接DF,设运动的时间为t秒(t≥0).

(1)直接写出用含t的代数式表示线段BE、EF的长;
(2)在这个运动过程中,△DEF能否为等腰三角形?若能,请求出t的值;若不能,请说明理由;
(3)设M、N分别是DF、EF的中点,求整个运动过程中,MN所扫过的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com