
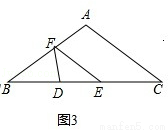
如图,在△ABC中,AB=AC=10cm,BC=16cm,DE=4cm.动线段DE(端点D从点B开始)沿BC边以1cm/s的速度向点C运动,当端点E到达点C时运动停止.过点E作EF∥AC交AB于点F(当点E与点C重合时,EF与CA重合),连接DF,设运动的时间为t秒(t≥0).

(1)直接写出用含t的代数式表示线段BE、EF的长;
(2)在这个运动过程中,△DEF能否为等腰三角形?若能,请求出t的值;若不能,请说明理由;
(3)设M、N分别是DF、EF的中点,求整个运动过程中,MN所扫过的面积.
(1)BE=(t+4)cm;EF=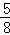 (t+4)cm;(2)当t=0、
(t+4)cm;(2)当t=0、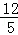 或
或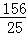 秒时,△DEF为等腰三角形;(3)整个运动过程中,MN所扫过的面积为
秒时,△DEF为等腰三角形;(3)整个运动过程中,MN所扫过的面积为 cm2.
cm2.
【解析】
试题分析:(1)由BD=tcm,DE=4cm,可得BE=BD+DE=(t+4)cm,又由EF∥AC,即可得△BEF∽△BAC,然后根据相似三角形的对应边成比例,即可求得EF的长;
(2)分三种情况讨论:①当DF=EF时,②当DE=EF时,③当DE=DF时,利用等腰三角形的性质与相似三角形的判定与性质,即可求得答案;
(3)首先设P是AC的中点,连接BP,可证得点B,N,P共线,即可得点N沿直线BP运动,MN也随之平移,设MN从ST位置运动到PQ位置,则四边形PQST是平行四边形,然后求得?PQST的面积即为MN所扫过的面积.
试题解析:(1)∵BD=tcm,DE=4cm,
∴BE=BD+DE=(t+4)cm,
∵EF∥AC,
∴△BEF∽△BCA,
∴EF:CA=BE:BC,
即EF:10=(t+4):16,
解得:EF=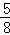 (t+4)(cm);
(t+4)(cm);
(2)分三种情况讨论:
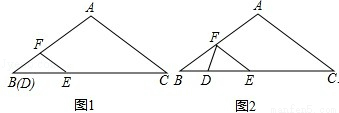
①如图1,∵当DF=EF时,
∴∠EDF=∠DEF,
∵AB=AC,
∴∠B=∠C,
∵EF∥AC,
∴∠DEF=∠C,
∴∠EDF=∠B,
∴点B与点D重合,
∴t=0;
②如图2,当DE=EF时,
则4=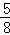 (t+4),
(t+4),
解得:t=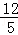 ;
;
③如图3,∵当DE=DF时,有∠DFE=∠DEF=∠B=∠C,
∴△DEF∽△ABC.
∴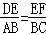 ,
,
即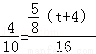 ,
,
解得:t=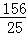 ;
;
综上所述,当t=0、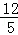 或
或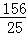 秒时,△DEF为等腰三角形.
秒时,△DEF为等腰三角形.
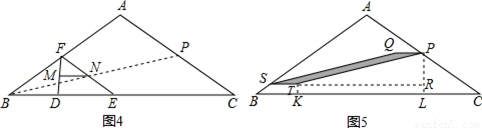
(3)如图4,设P是AC的中点,连接BP,
∵EF∥AC,
∴△FBE∽△ABC.
∴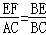 ,
,
∴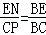 .
.
又∵∠BEN=∠C,
∴△NBE∽△PBC,
∴∠NBE=∠PBC.
∴点B,N,P共线,
∴点N沿直线BP运动,MN也随之平移.
如图5,设MN从ST位置运动到PQ位置,则四边形PQST是平行四边形.
∵M、N分别是DF、EF的中点,
∴MN∥DE,且ST=MN=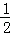 DE=2.
DE=2.
分别过点T、P作TK⊥BC,垂足为K,PL⊥BC,垂足为L,延长ST交PL于点R,则四边形TKLR是矩形,
∵当t=0时,EF=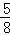 (0+4)=
(0+4)=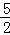 ,TK=
,TK= EFsin∠DEF=
EFsin∠DEF= •
•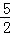 •
•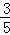 =
= ;
;
当t=12时,EF=AC=10,PL= AC•sin∠C=
AC•sin∠C= •10•
•10•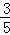 =3.
=3.
∴PR=PL﹣RL=PL﹣TK=3﹣ =
= .
.
∴S平行四边形PQST=ST•PR=2× =
= .
.
∴整个运动过程中,MN所扫过的面积为 cm2.
cm2.
考点:相似形综合题.


科目:初中数学 来源:2013-2014学年浙江省宁波市九年级上学期期中考试数学试卷(解析版) 题型:解答题
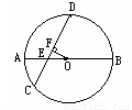
如图,⊙O的直径AB和弦CD相交于点E,已知AE=1cm,EB=5cm,∠DEB=600,求弦CD的长。
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省九年级直升班第一次综合测试数学试卷(解析版) 题型:填空题
如图,直线 A1A∥BB1∥CC1,若AB=8,BC=4,A1B1=6,则线段B1C1的长是_____________.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省九年级直升班第一次综合测试数学试卷(解析版) 题型:选择题
如图,半径为4的⊙O中有弦AB,以AB为折痕对折,劣弧恰好经过圆心O,则弦AB的长度等于( )

A、  B、4 C、
B、4 C、  D、
D、 
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省中考模拟数学试卷(解析版) 题型:解答题
体育课上,小明、小强、小华三人在学习训练踢足球,足球从一人传到另一人就记为踢一次.
(1)如果从小强开始踢,经过两次踢后,足球踢到了小华处的概率是多少(用树状图表示或列表说明);
(2)如果踢三次后,球踢到了小明处的可能性最小,应从谁开始踢?请说明理由.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年新疆阿拉尔市九年级秋季班第一次月考数学试卷(解析版) 题型:解答题
某商场销售一批名牌衬衫,平均每天可售出20件,每件盈利45元,为了扩大销售、增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出4件,若商场平均每天盈利2 100元,每件衬衫应降价多少元?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年广东省深圳市海怡翠学校九年级上学期期中考试数学试卷(解析版) 题型:选择题
函数 (
( 为常数)的图象上有三点(-4,
为常数)的图象上有三点(-4, ),(-1,
),(-1, ),(2,
),(2, ),则函数值
),则函数值 ,
, ,
, 的大小关系是( )
的大小关系是( )
A. <
< <
< B.
B. <
< <
< C.
C. <
< <
< D.
D. <
< <
<
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com