
【题目】如图,正方形ABCD的边长是2,点E是射线AB上一动点(点E与点A、B不重合),过点E作FG⊥DE交射线CB于点F、交DA的延长线于点G.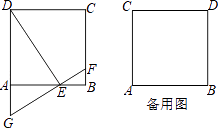
(1)求证:DE=GF.
(2)连结DF,设AE=x,△DFG的面积为y,求y与x之间的函数解析式.
(3)当Rt△AEG有一个角为30°时,求线段AE的长.
【答案】
(1)证明:过点F作FH⊥DA,垂足为H,
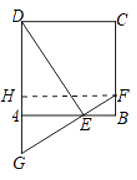
∵在正方形ABCD中,∠DAE=∠B=90°,
∴四边形ABFH是矩形,
∴FH=AB=DA,
∵DE⊥FG,
∴∠G=90°﹣∠ADE=∠DEA,
又∴∠DAE=∠FHG=90°,
∴△FHG≌△DAE,
∴DE=GF
(2)解:∵△FHG≌△DAE
∴FG=DE= ![]() ,
,
∵S△DGF= ![]() FGDE,
FGDE,
∴y= ![]() ,
,
∴解析式为:y= ![]() (0<x<2)
(0<x<2)
(3)解:①当∠AEG=30°时,
在Rt△ADE中,∵∠DAE=90°,AD=2,∠AED=90°﹣30°=60°,
∴AE=ADtan30°= ![]() ,
,
②当∠AEG=60°时,
在Rt△ADE中,∵∠DAE=90°,AD=2,∠AED=90°﹣60°=30°,
∴AE=ADtan60°=2 ![]() ,
,
综上所述,满足条件的AE的值为2 ![]() 或
或 ![]() .
.
【解析】(1)过点F作FH⊥DA,垂足为H,只要证明,△FHG≌△DAE即可解决问题;(2)由(1)可知DE=FG,所以△DGF的底与高可以关键勾股定理用含x的式子表示出来,所以解析式就可以表示出来;(3)分两种切线画出图形分别解决即可;
【考点精析】掌握正方形的性质是解答本题的根本,需要知道正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.
(1)填空:点A坐标为 ;抛物线的解析式为 .
(2)在图1中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时,点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图2中,若点P在对称轴上从点A开始向点B以1个单位/秒的速度运动,过点P做PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设置了两种促销方式.一种方式是:让顾客通过转转盘获得购物券.规定顾客每购买100元的商品,就能获得一次转转盘的机会,如果转盘停止后,指针正好对准100元、50元、20元的相应区域,那么顾客就可以分别获得100元、50元、20元购物券,凭购物券可以在该商场继续购物;如果指针对准其他区域,那么就不能获得购物券.另一种方式是:不转转盘,顾客每购买100元的商品,可直接获得10元购物券.据统计,一天中共有1 000人次选择了转转盘的方式,其中指针落在100元、50元、20元的次数分别为50次、100次、200次.
(1)指针落在不获奖区域的概率约是多少?
(2)通过计算说明选择哪种方式更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
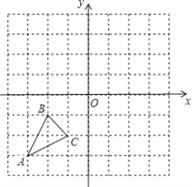
【题目】如图,已知A(﹣3,﹣3),B(﹣2,﹣1),C(﹣1,﹣2)是直角坐标平面上三点.
(1)请画出△ABC关于原点O对称的△A1B1C1;
(2)请写出点B关于y轴对称的点B2的坐标,若将点B2向上平移h个单位,使其落在△A1B1C1内部,指出h的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级(2)班40个学生某次数学测验成绩如下:
63,84,91,53,69,81,61,69,91,78,75,81,80,67,76,81,79,94,61,69,
89,70,70,87,81,86,90,88,85,67,71,82,87,75,87,95,53,65,74,77
数学老师按10分的组距分段,算出每个分数段学生成绩出现的频数,填入频数分页表:
(1)请把频数分布表、频数分布直方图补充完整并画出频数分布折线图;
(2)请你帮老师统计一下这次数学考试的及格率(60分以上含60分为及格)及优秀率(90分以上含90分为优秀);
(3)请说明哪个分数段的学生最多?哪个分数段的学生最少?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形纸片ABCD沿对角线BD折叠,设重叠部分为△EBD,则下列说法错误的是( ) 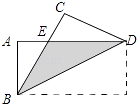
A.AB=CD
B.∠BAE=∠DCE
C.EB=ED
D.∠ABE一定等于30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次学科测验,学生得分均为整数,满分10分,成绩达到6分以上为合格.成绩达到9分为优秀.这次测验中甲乙两组学生成绩分布的条形统计图如下: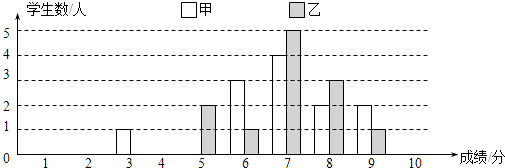
(1)请补充完成下面的成绩统计分析表:
平均分 | 方差 | 中位数 | 合格率 | 优秀率 | |
甲组 | 6.9 | 2.4 | 91.7% | 16.7% | |
乙组 | 1.3 | 83.3% | 8.3% |
(2)甲组学生说他们的合格率、优秀率均高于乙组,所以他们的成绩好于乙组.但乙组学生不同意甲组学生的说法,认为他们组的成绩要高于甲组.请你给出三条支持乙组学生观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
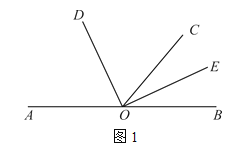
【题目】已知,O为直线AB上一点,∠DOE=90°.
(1)如图1,若∠AOC=130°,OD平分∠AOC.
①求∠BOD的度数;
②请通过计算说明OE是否平分∠BOC.
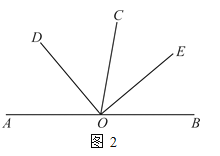
(2)如图2,若∠BOE:∠AOE=2:7,求∠AOD的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com