
【题目】如图:在平行四边形ABCD中,用直尺和圆规作∠BAD的平分线交BC于点E(尺规作图的痕迹保留在图中了),连接EF.
(1)求证:四边形ABEF为菱形;
(2)AE,BF相交于点O,若BF=6,AB=5,求AE的长.

科目:初中数学 来源: 题型:
【题目】将抛物线向上平移2个单位长度,再向右平移3个单位长度后得到y=﹣(x﹣2)2+3,则原抛物线的解析式为( )
A.y=﹣(x+1)2+1B.y=﹣(x﹣1)2﹣1
C.y=﹣x2D.y=﹣(x﹣5)2+5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将抛物线y=x2向上平移2个单位后,所得的抛物线的函数表达式为( )
A.y=x2+2
B.y=x2﹣2
C.y=(x+2)2
D.y=(x﹣2)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是2,点E是射线AB上一动点(点E与点A、B不重合),过点E作FG⊥DE交射线CB于点F、交DA的延长线于点G.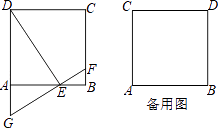
(1)求证:DE=GF.
(2)连结DF,设AE=x,△DFG的面积为y,求y与x之间的函数解析式.
(3)当Rt△AEG有一个角为30°时,求线段AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某个体户购进一批时令水果,20天销售完毕.他将本次销售情况进行了跟踪记录,根据所记录的数据可绘制的函数图象,其中日销售量y(千克)与销售时间x(天)之间的函数关系如图甲所示,销售单价p(元/千克)与销售时间x(天)之间的函数关系如图乙所示. 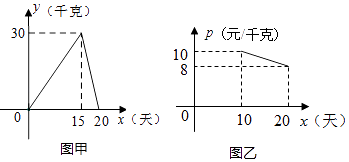
(1)直接写出y与x之间的函数关系式;
(2)分别求出第10天和第15天的销售金额;
(3)若日销售量不低于24千克的时间段为“最佳销售期”,则此次销售过程中“最佳销售期”共有多少天?在此期间销售单价最高为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.
(1)如图1,当点Q在DC边上时,探究PB与PQ所满足的数量关系; 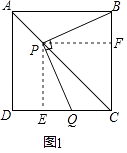
小明同学探究此问题的方法是:
过P点作PE⊥DC于E点,PF⊥BC于F点,
根据正方形的性质和角平分线的性质,得出PE=PF,
再证明△PEQ≌△PFB,可得出结论,他的结论应是
(2)如图2,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想. 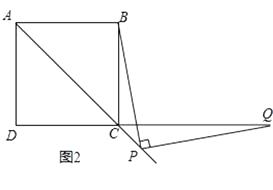
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com