
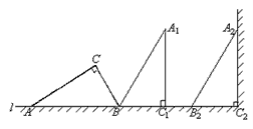
【题目】如图,在一个横截面为Rt△ABC的物体中,∠ACB=90°,∠CAB=30°,BC=1米。工人师傅把此物体搬到墙边,先将AB边放在地面(直线l)上,再按顺时针方向绕点B翻转到△A1B1C1的位置(BC1在L上),最后沿BC1的方向平移到△A2B2C2的位置,其平移的距离为线段AC的长度(此时A2C2恰好靠在墙边)。
(1)求出AB的长;
(2)求出AC的长;
(3)画出在搬动此物的整个过程A点所经过的路径,并求出该路径的长度(精确到0.1米)。
【答案】(1) AB=2米; (2)AC=![]() 米;(3)画图见解析;
米;(3)画图见解析;![]() .
.
【解析】
试题(1)(2)根据直角三角形的三边关系,30°的角所对的直角边是斜边的一半,可以直接确定AB、AC.
(3)根据要求画出路径,再用弧长公式求解路径的长度.根据题意得到Rt△ABC在直线l上转动两次点A分别绕点B旋转120°和绕C旋转90°,将两条弧长求出来加在一起即可.
试题解析:(1)(2)∵∠CAB=30°,BC=1米
∴AB=2米,AC=![]() 米.
米.
(3)画出A点经过的路径:
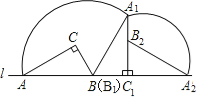
∵∠ABA1=180°-60°=120°,A1A2=AC=![]() 米
米
∴A点所经过的路径长=![]() (米).
(米).
(3)在Rt△ABC中,∵BC=1,AC=![]()
∴AB=2,∠CBA=60°,
∴![]() ,
,![]() ,
,
∴点A经过的路线的长是![]() .
.
故两次翻转此物的整个过程点A经过路径的长度为是![]() .
.
考点: 1.弧长的计算;2.旋转的性质;3.解直角三角形.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,要把残破的轮片复制完整,已知弧上的三点A、B、C.
①用尺规作图法找出![]() 所在圆的圆心(保留作图痕迹,不写作法);
所在圆的圆心(保留作图痕迹,不写作法);
②设△ABC是等腰三角形,底边BC=8cm,腰AB=5cm,求圆片的半径R.

查看答案和解析>>
科目:初中数学 来源: 题型:
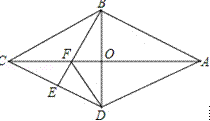
【题目】如图,在四边形ABCD中,AB=AD,CB=CD,AC与BD相交于O点,OC=OA,若E是CD上任意一点,连接BE交AC于点F,连接DF.
(1)证明:△CBF≌△CDF;
(2)若AC=2![]() ,BD=2,求四边形ABCD的周长。
,BD=2,求四边形ABCD的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB与弦CD交于点,AE=6,BE=2,CD=2![]() ,则∠AED的度数是( )
,则∠AED的度数是( )
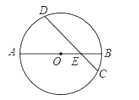
A. 30° B. 60° C. 45° D. 36°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用指定的方法解下列一元二次方程:
(1)x2﹣2x﹣2=0(公式法);
(2)2(x﹣3)=3x(x﹣3)(因式分解法);
(3)2x2﹣4x+1=0(配方法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个可以自由转动的转盘被平均分成3个扇形,分别标有1、2、3三个数字,小王和小李各转动一次转盘为一次游戏,当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束得到一组数(若指针指在分界线时重转).
(1)请你用树状图或列表的方法表示出每次游戏可能出现的所有结果;
(2)求每次游戏结束得到的一组数恰好是方程x2﹣3x+2=0的解的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:

①△ABE≌△ACF;②BC=DF;③S△ABC=S△ACF+S△DCF;④若BD=2DC,则GF=2EG.其中正确的结论是 .(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.

(1)求女生进球数的平均数、中位数;
(2)投球4次,进球3个以上(含3个)为优秀,全校有女生1200人,估计为“优秀”等级的女生约为多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com