
【题目】如图,有一个可以自由转动的转盘被平均分成3个扇形,分别标有1、2、3三个数字,小王和小李各转动一次转盘为一次游戏,当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束得到一组数(若指针指在分界线时重转).
(1)请你用树状图或列表的方法表示出每次游戏可能出现的所有结果;
(2)求每次游戏结束得到的一组数恰好是方程x2﹣3x+2=0的解的概率.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC>AB>AC.甲、乙两人想在BC上取一点P,使得∠APC=2∠ABC,其作法如下:
(甲)作AB的中垂线,交BC于P点,则P即为所求;
(乙)以B为圆心,AB长为半径画弧,交BC于P点,则P即为所求.
对于两人的作法,下列判断何者正确?( )
![]()
A. 两人皆正确B. 两人皆错误C. 甲正确,乙错误D. 甲错误,乙正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-(2k+3)+k2+3k-4=0.
(1) 试判断上述方程根的情况并说明理由;
(2) 若以上一元二次方程的两个根分别为![]() 、
、![]() (
(![]() ),
),
① m=________,n=_________;
②当![]() 时,点A、B分别是直线
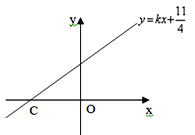
时,点A、B分别是直线![]() :y=kx+
:y=kx+![]() 上两点且A、B两点的横坐标分别为
上两点且A、B两点的横坐标分别为![]() 、
、![]() ,直线
,直线![]() 与
与![]() 轴相交于点C,若S△BOC=2S△AOC,求
轴相交于点C,若S△BOC=2S△AOC,求![]() 的值;
的值;
(3)在(2)的条件下,问在![]() 轴上是否存在点Q,使△ABQ的三个内角平分线交点在
轴上是否存在点Q,使△ABQ的三个内角平分线交点在![]() 轴上?若存在,求出点Q的坐标,若不存在,请说明理由.
轴上?若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD在直角坐标系中,边BC在x轴上,B点坐标为(m,0)且m>0.AB=a,BC=b,且满足b=![]() .
.
(1)求a,b的值及用m表示出点D的坐标;
(2)连接OA,AC,若△OAC为等腰三角形,求m的值;
(3)△OAC能为直角三角形吗?若能,求出m的值;若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从2018年高中一年级学生开始,湖南省全面启动高考综合改革,学生学习完必修课程后,可以根据高校相关专业的选课要求和自身兴趣、志向、优势,从思想政治、历史、地理、物理、化学、生物6个科目中,自主选择3个科目参加等级考试.学生![]() 已选物理,还想从思想政治、历史、地理3个文科科目中选1科,再从化学、生物2个理科科目中选1科.若他选思想政治、历史、地理的可能性相等,选化学、生物的可能性相等,则选修地理和生物的概率为___________.
已选物理,还想从思想政治、历史、地理3个文科科目中选1科,再从化学、生物2个理科科目中选1科.若他选思想政治、历史、地理的可能性相等,选化学、生物的可能性相等,则选修地理和生物的概率为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=45°,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,且EH=EB.下列四个结论:①∠ABC=45°;②AH=BC;③BE+CH=AE;④△AEC是等腰直角三角形.你认为正确的序号是( )

A. ①②③ B. ①③④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个整数能表示成a2+b2(a、b是正整数)的形式,则称这个数为“丰利数”.例如,2是“丰利数”,因为2=12+12,再如,M=x2+2xy+2y2=(x+y)2+y2(x+y,y是正整数),所以M也是“丰利数”.
(1)请你写一个最小的三位“丰利数”是 ,并判断20 “丰利数”.(填是或不是);
(2)已知S=x2+y2+2x﹣6y+k(x、y是整数,k是常数),要使S为“丰利数”,试求出符合条件的一个k值(10≤k<200),并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
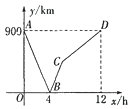
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km).图中的折线表示y与x之间的函数关系.根据图象进行以下探究:
(1)甲、乙两地之间的距离为_________km;
(2)求慢车和快车的速度;
(3)请解释图中点C的实际意义;
(4)分别写出线段AB、BC所表示的y与x之间的函数关系式;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com