
【题目】如图,⊙O的直径AB与弦CD交于点,AE=6,BE=2,CD=2![]() ,则∠AED的度数是( )
,则∠AED的度数是( )
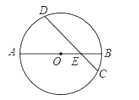
A. 30° B. 60° C. 45° D. 36°
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】一袋装有编号为1,2,3的三个形状、大小、材质等相同的小球,从袋中随意摸出1个球,记事件A为“摸出的球编号为奇数”,随意抛掷一个之地均匀正方体骰子,六个面上分别写有1﹣6这6个整数,记事件B为“向上一面的数字是3的整数倍”,请你判断等式“P(A)=2P(B)”是否成立,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),直线![]() 与x轴交于点A、与y轴交于点D,以AD为腰,以x轴为底作等腰梯形ABCD(AB>CD),且等腰梯形的面积是8
与x轴交于点A、与y轴交于点D,以AD为腰,以x轴为底作等腰梯形ABCD(AB>CD),且等腰梯形的面积是8![]() ,抛物线经过等腰梯形的四个顶点.
,抛物线经过等腰梯形的四个顶点.
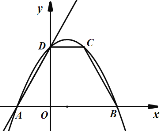
图(1)
(1) 求抛物线的解析式;
(2) 如图(2)若点P为BC上的—个动点(与B、C不重合),以P为圆心,BP长为半径作圆,与![]() 轴的另一个交点为E,作EF⊥AD,垂足为F,请判断EF与⊙P的位置关系,并给以证明;
轴的另一个交点为E,作EF⊥AD,垂足为F,请判断EF与⊙P的位置关系,并给以证明;
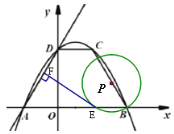
图(2)
(3) 在(2)的条件下,是否存在点P,使⊙P与y轴相切,如果存在,请求出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直线![]() 的函数解析式为
的函数解析式为![]() ,与
,与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
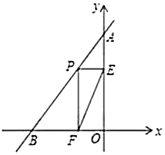
(1)直接写出点![]() 的坐标________;
的坐标________;![]() 点的坐标________;
点的坐标________;
(2)若点![]() 为线段
为线段![]() 上的一个动点,作
上的一个动点,作![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() ,连接
,连接![]() ,问:①若
,问:①若![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式;②直接写出
的函数关系式;②直接写出![]() 的最小值________;
的最小值________;
查看答案和解析>>
科目:初中数学 来源: 题型:
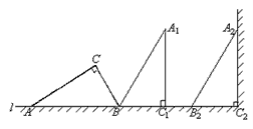
【题目】如图,在一个横截面为Rt△ABC的物体中,∠ACB=90°,∠CAB=30°,BC=1米。工人师傅把此物体搬到墙边,先将AB边放在地面(直线l)上,再按顺时针方向绕点B翻转到△A1B1C1的位置(BC1在L上),最后沿BC1的方向平移到△A2B2C2的位置,其平移的距离为线段AC的长度(此时A2C2恰好靠在墙边)。
(1)求出AB的长;
(2)求出AC的长;
(3)画出在搬动此物的整个过程A点所经过的路径,并求出该路径的长度(精确到0.1米)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2m+1)x+m2﹣2=0.
(1)若该方程有两个实数根,求m的最小整数值;
(2)若方程的两个实数根为x1,x2,且(x1﹣x2)2+m2=21,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王老师将1个黑球和若干个白球(这些球除颜色外都相同)放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出1个球(有放回),下表是活动进行中的一组统计数据.
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸出黑球的次数m | 23 | 31 | 60 | 130 | 203 | 251 |
摸到黑球的频率 | 0.23 | 0.207 | 0.30 | 0.26 | 0.254 | 0.251 |
(1)根据上表数据估计从袋中摸出1个球是黑球的概率是_________;
(2)估计袋中白球的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
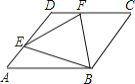
【题目】如图,在边长为1的菱形ABCD中,DAB 60°,E是AD上不同于A,D两点的一动点,F是CD上一点,且AECF1.
(1)证明:无论E,F怎样移动,BEF总是等边三角形;
(2)求BEF 面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com