
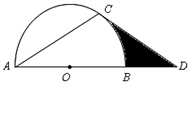
 如图,点
如图,点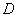 在
在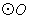 的直径
的直径 的延长线上,点
的延长线上,点 在
在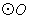 上,且
上,且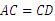 ,
,
∠ °.
°.
(1)求证: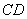 是
是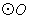 的切线;
的切线;
(2)若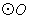 的半径为2,求图中阴影部分的面积.
的半径为2,求图中阴影部分的面积.
科目:初中数学 来源: 题型:
在一个袋子中,有完全相同的4张卡片,把它们分別编码为1,2,3,4.
(1)从袋子中随机取两张卡片,求取出的卡片的编号之和等于5的概率;
(2)先从袋子中随机取一张卡片,记该卡片的编号为m,然后将其放回袋中,再从袋中随机取出一张卡片,记该卡片的编号为n,求满足m+1>n的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
九(1)班数学兴趣小组经 过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
| 时间x(天) | 1≤x<50 | 50≤x≤90 |
| 售价(元/件) | x+40 | 90 |
| 每天销量(件) | 200﹣2x |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?
查看答案和解析>>
科目:初中数学 来源: 题型:
填空,完成下列说理过程
如图,点A,O,B在同一条直线上, OD,OE分别平分∠AOC和∠BOC.
(1)求∠DOE的度数;
(2)如果∠COD=65°,求∠AOE的度数.
 解:(1)如图,因为OD是∠AOC的平分线,
解:(1)如图,因为OD是∠AOC的平分线,
所以∠COD = ∠AOC.
∠AOC.
因为OE是∠BOC 的平分线,
所以 = ∠BOC.
∠BOC.
所以∠DOE=∠COD+ = (∠AOC+∠BOC)=
(∠AOC+∠BOC)= ∠AOB= °.
∠AOB= °.
(2)由(1)可知
∠BOE=∠COE = -∠COD= °.
所以∠AOE= -∠BOE= °.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com