
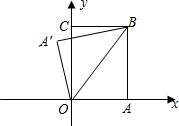
 如图,矩形OABC,tan∠AOB=
如图,矩形OABC,tan∠AOB=| 4 |
| 3 |
| k |
| x |
 ,
,| AB |
| OA |
| 4 |
| 3 |
| 2tan∠AOB |
| 1-tan2∠AOB |
2×
| ||
1-(
|
| 24 |
| 7 |
| 24 |
| 7 |
| 6 |
| 25 |
| 42 |
| 25 |
| 144 |
| 25 |
| 42 |
| 25 |
| 144 |
| 25 |
| k |
| x |
| 42 |
| 25 |
| 144 |
| 25 |
| 6048 |
| 625 |
| ||
| x |
| ||
| x |


科目:初中数学 来源: 题型:
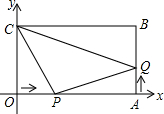 如图,在平面直角坐标系中,矩形OABC的两边分别在x轴和y轴上,OA=10厘米,OC=6厘米,现有两动点P,Q分别从O,A同时出发,点P在线段OA上以1厘米/秒的速度沿OA方向作匀速运动,点Q在线段AB上以
如图,在平面直角坐标系中,矩形OABC的两边分别在x轴和y轴上,OA=10厘米,OC=6厘米,现有两动点P,Q分别从O,A同时出发,点P在线段OA上以1厘米/秒的速度沿OA方向作匀速运动,点Q在线段AB上以| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 哈西客站投入使用以来,每天输送了大量的旅客.某日,从早8点开始到上午11点,为了缓解旅客压力,在原来基础上新增了3个售票窗口,每个售票窗口售出的车票数y(张)与售票时间x(小时)的关系满足如图所示的图象,其中OA为原有窗口,OB为新增窗口.
哈西客站投入使用以来,每天输送了大量的旅客.某日,从早8点开始到上午11点,为了缓解旅客压力,在原来基础上新增了3个售票窗口,每个售票窗口售出的车票数y(张)与售票时间x(小时)的关系满足如图所示的图象,其中OA为原有窗口,OB为新增窗口.查看答案和解析>>
科目:初中数学 来源: 题型:
| 7 |
| 8 |
| 3 |
| 4 |
| 23 |
| 24 |
| 1 |
| 2 |
| 5 |
| 6 |
| 7 |
| 12 |
| 1 |
| 36 |
| 1 |
| 2 |
| 1 |
| 8 |
| 5 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com