
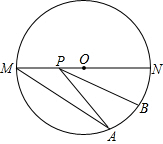
 如图,已知⊙O的直径MN=1,点A在圆上,且∠AMN的度数为30°,点B是弧AN的中点,点P在直径MN上运动,求BP+AP的最小值为$\frac{\sqrt{2}}{2}$.
如图,已知⊙O的直径MN=1,点A在圆上,且∠AMN的度数为30°,点B是弧AN的中点,点P在直径MN上运动,求BP+AP的最小值为$\frac{\sqrt{2}}{2}$. 分析 过B作关于直线MN的对称点B′,连接AB′,由轴对称的性质可知AB′即为PA+PB的最小值,由同弧所对的圆心角和圆周角的性质可知∠AON=2∠AMN=2×30°=60°,由对称的性质可知∠B′ON=∠BON=30°,即可求出∠AOB′的度数,再由勾股定理即可求解.
解答 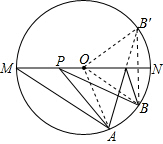 解:作点B关于MN的对称点B′,连接OA、OB、OB′、AB′,
解:作点B关于MN的对称点B′,连接OA、OB、OB′、AB′,
则AB′与MN的交点即为PA+PB的最小时的点,PA+PB的最小值=AB′,
∵∠AMN=30°,
∴∠AON=2∠AMN=2×30°=60°,
∵点B为劣弧AN的中点,
∴∠BON=∠AON=$\frac{1}{2}$×60°=30°,
由对称性,∠B′ON=∠BON=30°,
∴∠AOB′=∠AON+∠B′ON=60°+30°=90°,
∴△AOB′是等腰直角三角形,
∴AB′=$\sqrt{2}$OA=$\sqrt{2}$×$\frac{1}{2}$=$\frac{\sqrt{2}}{2}$,
即PA+PB的最小值=$\frac{\sqrt{2}}{2}$.
故答案为$\frac{\sqrt{2}}{2}$.
点评 本题考查的是圆周角定理及勾股定理,解答此题的关键是根据题意作出辅助线,构造出直角三角形,利用勾股定理求解.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
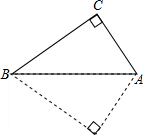 如图,Rt△ABC中,∠C=90°,将△ABC沿AB向下翻折后,再绕点A顺时针旋转角度α(α<∠BAC),得到Rt△AED,其中斜边AE交BC于点F,直角边DE分别交AB,BC于点G,H.
如图,Rt△ABC中,∠C=90°,将△ABC沿AB向下翻折后,再绕点A顺时针旋转角度α(α<∠BAC),得到Rt△AED,其中斜边AE交BC于点F,直角边DE分别交AB,BC于点G,H.查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省苏州太仓市第二学期初一期中复习检测数学试卷(一)(解析版) 题型:单选题
如果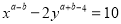 是二元一次方程,那么
是二元一次方程,那么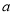 、
、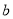 的值分别是( )
的值分别是( )
A. 3、1 B. 3、2 C. 2、1 D. 2、-1
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com