
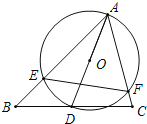
【题目】如图,△ABC中,∠BAC=60°,∠ABC=45°,AB=![]() ,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值为 .
,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值为 .
【答案】![]()
【解析】
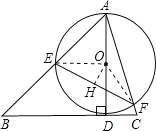
试题分析:由垂线段的性质可知,当AD为△ABC的边BC上的高时,直径最短,如图,连接OE,OF,过O点作OH⊥EF,垂足为H,由Rt△ADB为等腰直角三角形,则AD=BD=1,即此时圆的直径为1,再根据圆周角定理可得到∠EOH=60°,则在Rt△EOH中,利用锐角三角函数可计算出EH=![]() ,然后根据垂径定理即可得到EF=2EH=
,然后根据垂径定理即可得到EF=2EH=![]() .
.
解:由垂线段的性质可知,当AD为△ABC的边BC上的高时,直径最短,
如图,连接OE,OF,过O点作OH⊥EF,垂足为H,
在Rt△ADB中,∠ABC=45°,AB=![]() ,
,
∴AD=BD=1,即此时圆的直径为1,
∵∠EOF=2∠BAC=120°,
而∠EOH=∠EOF,
∴∠EOH=60°,
在Rt△EOH中,EH=OEsin∠EOH=![]() sin60°=
sin60°=![]() ,
,
∵OH⊥EF,
∴EH=FH,
∴EF=2EH=![]() ,
,
即线段EF长度的最小值为![]() .
.
故答案为![]() .
.


 全能练考卷系列答案
全能练考卷系列答案科目:初中数学 来源: 题型:
【题目】下列四组条件中, 能使△ABC≌△DEF的条件有( )
①AB = DE, BC = EF, AC = DF; ②AB = DE, ∠B = ∠E, BC = EF;
③∠B = ∠E, BC = EF, ∠C = ∠F; ④AB = DE, AC = DF, ∠B = ∠E.
A. 1组 B. 2组 C. 3组 D. 4组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C是线段AB的中点,CD平分∠ACE,CE平分∠BCD,CD=CE;
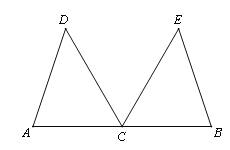
(1)求证:△ACD≌△BCE;
(2)若∠D=50°,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一定在△ABC内部的线段是( )
A. 锐角三角形的三条高、三条角平分线、三条中线
B. 钝角三角形的三条高、三条中线、一条角平分线
C. 任意三角形的一条中线、二条角平分线、三条高
D. 直角三角形的三条高、三条角平分线、三条中线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com