
【题目】如图,长方形ABCD中,AB=2,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.当△CEB′为直角三角形时,BE的长为__.

【答案】2或![]()
【解析】
当△CEB′为直角三角形时,有两种情况:①当点B′落在矩形内部时,如答图1所示.连结AC,先利用勾股定理计算出AC=![]() ,根据折叠的性质得∠AB′E=∠B=90°,而当△CEB′为直角三角形时,只能得到∠EB′C=90°,所以点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,则EB=EB′,AB=AB′=2,可计算出CB′=
,根据折叠的性质得∠AB′E=∠B=90°,而当△CEB′为直角三角形时,只能得到∠EB′C=90°,所以点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,则EB=EB′,AB=AB′=2,可计算出CB′=![]() -2,设BE=x,则EB′=x,CE=4-x,然后在Rt△CEB′中运用勾股定理可计算出x.②当点B′落在AD边上时,如答图2所示.此时ABEB′为正方形.
-2,设BE=x,则EB′=x,CE=4-x,然后在Rt△CEB′中运用勾股定理可计算出x.②当点B′落在AD边上时,如答图2所示.此时ABEB′为正方形.
解:当△CEB′为直角三角形时,有两种情况:
①当点B′落在矩形内部时,如答图1所示.
连结AC,
在Rt△ABC中,AB=2,BC=4,
∴![]() ,
,
∵∠B沿AE折叠,使点B落在点B′处,
∴∠AB′E=∠B=90°,
当△CEB′为直角三角形时,只能得到∠EB′C=90°,
∴点A、B′、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点B′处,
∴EB=EB′,AB=AB′=2,
∴CB′=![]() ,
,
设BE=x,则EB′=x,CE=4-x,
在Rt△CEB′中,
∵EB′2+CB′2=CE2,
∴![]()
即:![]() ,
,
解得:![]() ;
;
②当点B′落在AD边上时,如答图2所示.
此时ABEB′为正方形,
∴BE=AB=2.
故答案为:2或![]() ;
;


科目:初中数学 来源: 题型:
【题目】新个税法于2018年1月1日起施行,2018年10月1日起施行最新“起征点:5000元”和税率,《中华共和国个人所得税》中的个人所得税税率如下:
级数 | 全月应纳税所得额 | 税率(%) |
1 | 不超过3000元的部分 | 3 |
2 | 超过3000元至12000元的部分 | 10 |
3 | 超过12000元至25000元的部分 | 20 |
其中“全月应纳税所得额”是指从工资、薪金收入中减去5000元后的金额。(本题只讨论上表内容)
(1)若某一月份扣除税后拿了8000,他交了多少税?
(2)若某一月份纳税额为m元(m>0),他的税前收入是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列例题的解题过程,再解答下面问题
例题:已知 m n 100 , x y 1 ,求 n x m y 的值
解: n x m y n x m y m n x y 100 1 101
问题:(1)已知 a b 7 , ab 10 ,求 3ab 6a 4b 2a 2ab 的值;
(2)已知 a 2 2ab 2, ab b2 4, 求2a 2 ![]() ab
ab ![]() b2
b2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2013年9月23日强台风“天兔”登录深圳,伴随着就是狂风暴雨。梧桐山山坡上有一棵与水平面垂直的大树,台风过后,大树被刮倾斜后折断倒在山坡上,树的顶部恰好接触到坡面(如图所示)。已知山坡的坡角∠AEF=23°,量得树干的倾斜角为∠BAC=38°,大树被折断部分和坡面所成的角∠ADC=60°, AD=3m。
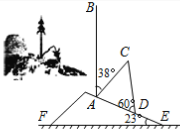
(1)求∠DAC的度数;
(2)求这棵大树折断前的高度。(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为确保信息安全,信息需加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密).安全员是数学爱好者,制定加密规则为:明文x,y,z对应密文x+y+z,x-y+z,x-y-z.例如:明文1,2,3对应密文6,2,-4.当接收方收到密文12,4,-6时,则解密得到的明文为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某沿海城市A接到台风警报,在该市正南方向![]() 千米有一台风中心正在B处形成,并沿着北偏东45°的BC方向以15千米/小时的速度向C移动,AD⊥BC于D,如果在距台风中心150千米的区域内都将受到台风的影响,请问:
千米有一台风中心正在B处形成,并沿着北偏东45°的BC方向以15千米/小时的速度向C移动,AD⊥BC于D,如果在距台风中心150千米的区域内都将受到台风的影响,请问:

(1)通过计算说明,台风会否影响到A市?
(2)画图计算说明,台风中心从B处出发后,经过几小时会影响到A市,对A市持续影响的时间有多少小时?在第几小时时对A市的影响最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:善于思考的小明在解方程组 时,采用了一种“整体代换”的解法,解法如下:
时,采用了一种“整体代换”的解法,解法如下:
解:将方程②8x+20y+2y=10,变形为2(4x+10y)+2y=10③,把方程①代入③得,2×6+2y=10,则y=-1;把y=-1代入①得,x=4,所以方程组的解为:![]() ,
,
请你解决以下问题:
(1)试用小明的“整体代换”的方法解方程组
(2)已知x、y、z,满足 试求z的值.
试求z的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校随机对本校部分学生进行“假期中,我在家可以这么做:![]() .扎实学习、
.扎实学习、![]() .快乐游戏、
.快乐游戏、![]() .经典阅读、
.经典阅读、![]() .分担劳动、
.分担劳动、![]() .乐享健康”网络调查,并根据调查结果绘制成如下两幅不完整的统计图(若每一位同学只能选择一项),请根据图中信息,回答下列问题.
.乐享健康”网络调查,并根据调查结果绘制成如下两幅不完整的统计图(若每一位同学只能选择一项),请根据图中信息,回答下列问题.

(1)这次调查的总人数是___________人;
(2)请补全条形统计图,并说明扇形统计图中![]() 所对应的圆心角是___________度;
所对应的圆心角是___________度;
(3)若该学校共有学生1700人,则选择![]() 有多少人?
有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
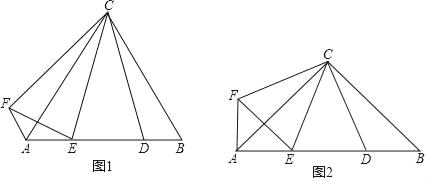
【题目】(1)操究发现:如图1,△ABC为等边三角形,点D为AB边上的一点,∠DCE=30°,∠DCF=60°且CF=CD
①求∠EAF的度数;
②DE与EF相等吗?请说明理由
(2)类比探究:如图2,△ABC为等腰直角三角形,∠ACB=90°,点D为AB边上的一点,∠DCE=45°,CF=CD,CF⊥CD,请直接写出下列结果:
①∠EAF的度数
②线段AE,ED,DB之间的数量关系
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com