Question

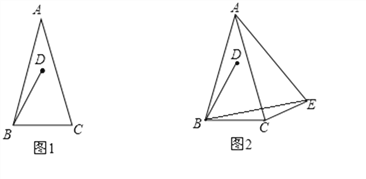
【题目】在△ABC中，AB=AC，∠BAC=α（0°＜α＜60°），点D在△ABC内，且BD=BC,∠DBC=60°.

（1）如图1， 连接AD,直接写出∠ABD的度数（用含α的式子表示）；

（2）如图2，∠BCE=150°，∠ABE=60°，判断△ABE的形状并加以证明；

（3）在（2）的条件下，连接DE，若∠DEC=45°，求α的值．

Answer 1

【答案】(1)30°- ;(2) △ABE是等边三角形,证明见解析；（3）30°.

【解析】试题分析：（1）求出∠ABC的度数，即可求出答案；

（2）连接AD，CD，ED，根据旋转性质得出BC=BD，∠DBC=60°，求出∠ABD=∠EBC=30°-α，且△BCD为等边三角形，证△ABD≌△ACD，推出∠BAD=∠CAD=∠BAC=α，求出∠BEC=α=∠BAD，证△ABD≌△EBC，推出AB=BE即可；

（3）求出∠DCE=90°，△DEC为等腰直角三角形，推出DC=CE=BC，求出∠EBC=15°，得出方程30°-α=15°，求出即可．

试题解析：（1）（1）∵AB=AC，∠A=α，

∴∠ABC=∠ACB=（180°-∠A）=90°-α，

∵∠ABD=∠ABC-∠DBC，∠DBC=60°，

即∠ABD=30°-α；

（2）△ABE是等边三角形，理由如下：

连接AD，CD，

∵∠ABE=60°， ∠ABD=30°- ，

∴∠DBE=30°+ ，

又∵∠DBC=60°，

∴∠CBE=30°- =∠ABD，

∵∠DBC=60°，BD=BC，

∴△BDC是等边三角形，

∴BD=CD，

在△ABD和△ACD中，AB=AC，BD=CD，AD=AD，

∴△ABD≌△ACD，

∴∠BAD=∠CAD= ，

在△BCE中，∠BCE=150°，∠CBE=30°- ，

∴∠BEC= =∠BAD，

在△ABD和△CBE中， ∠BEC=∠BAD， ∠CBE=∠ABD，AB=AC，

∴△ABD≌△CBE，

∴AB=BE，

又∵∠ABE=60°，

∴△ABE是等边三角形；

（3）由(2)知△BDC是等边三角形，

∴∠BCD=60°，

∵∠BCE=150°，

∴∠DCE=90°，

∵∠DEC=45°，

∴△DCE是等腰直角三角形，

∴CD=CE=BC，在△BCE中， ∠BCE=150°，

∴∠CBE=30°- =15°，

∴a=30°.