
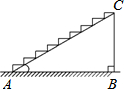
 如图所示:是一段楼梯,高BC是5m,斜边AC是13m,如果在楼梯上铺地毯,那么至少需要地毯17米.
如图所示:是一段楼梯,高BC是5m,斜边AC是13m,如果在楼梯上铺地毯,那么至少需要地毯17米.  津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (+6)+(-13)=+7 | B. | (+6)+(-13)=-19 | C. | (+6)+(-13)=-7 | D. | (-5)+(-3)=8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
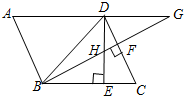 如图,平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE,BF相交于H,BF,AD的延长线相交于G,下面结论:①DB=$\sqrt{2}$BE,②△BHE∽△BCF,③AB=BH,④△BHD∽△BDG,其中正确的结论是( )
如图,平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,DE,BF相交于H,BF,AD的延长线相交于G,下面结论:①DB=$\sqrt{2}$BE,②△BHE∽△BCF,③AB=BH,④△BHD∽△BDG,其中正确的结论是( )| A. | ①②③④ | B. | ①②③ | C. | ①②④ | D. | ②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,将1,$\sqrt{2},\sqrt{3}$,$\sqrt{6}$按照如图方式排列,若规定(m,n)表示第m排从左向右的第n个数,则(15,7)表示的数是$\sqrt{6}$.
如图,将1,$\sqrt{2},\sqrt{3}$,$\sqrt{6}$按照如图方式排列,若规定(m,n)表示第m排从左向右的第n个数,则(15,7)表示的数是$\sqrt{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com