
| a2+c2-b2 |
| 2ac |
| a2+c2-b2 |
| 2ac |


 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
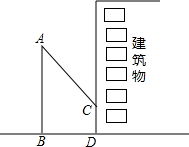 小明想利用校园内松树的树影测量树的高度,他在某一时刻测得长为1m的侧杆的影长为0.9m,但当他要测松树的影长时,因为树的影子恰好有一部分落在一座建筑物的墙上,如图所示,他先测得松树留在墙上的影子高CD=1.2m,又测得松树在地面上的影长BD=2.7m,请你帮助小明求出松树的高度.
小明想利用校园内松树的树影测量树的高度,他在某一时刻测得长为1m的侧杆的影长为0.9m,但当他要测松树的影长时,因为树的影子恰好有一部分落在一座建筑物的墙上,如图所示,他先测得松树留在墙上的影子高CD=1.2m,又测得松树在地面上的影长BD=2.7m,请你帮助小明求出松树的高度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com