
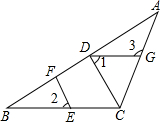
 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F. 分析 (1)根据CD⊥AB,EF⊥AB,得出∠BFE=∠BDC=90°,再根据同位角相等,两直线平行可直接得出CD∥EF;
(2)根据CD∥EF,得出∠2=∠ECD,再根据∠1=∠2,得出∠1=∠ECD,从而得出DG∥BC,再根据两直线平行,同位角相等得出∠3=∠ACB,即可求出∠ACB的度数.
解答 解:(1)∵CD⊥AB,EF⊥AB,
∴∠BFE=∠BDC=90°,
∴CD∥EF;
(2)∵CD∥EF,
∴∠2=∠ECD,
∵∠1=∠2,
∴∠1=∠ECD,
∴DG∥BC,
∴∠3=∠ACB,
∵∠3=95°,
∴∠ACB=95°.
点评 此题考查了平行线的判定与性质:同位角相等,两直线平行;内错角相等,两直线平行;两直线平行,同位角相等;熟练掌握平行线的判定与性质是解题的关键.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:解答题
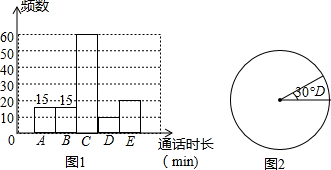 现如今,收集已成为人们普遍的交流工具,人们用它来打电话、上网.为了解3月份某单位职工的本地通话时长,随机抽取了该单位职工的通话时长进行抽样调查,将调查结果分成为A,B,C,D五个组,并利用所得数据绘制了如图1所示的频数分布直方图和如图2所示的不完整的扇形统计图.
现如今,收集已成为人们普遍的交流工具,人们用它来打电话、上网.为了解3月份某单位职工的本地通话时长,随机抽取了该单位职工的通话时长进行抽样调查,将调查结果分成为A,B,C,D五个组,并利用所得数据绘制了如图1所示的频数分布直方图和如图2所示的不完整的扇形统计图. | 组别 | 通话时长(min) |
| A | x<100 |
| B | 100≤x<200 |
| C | 200≤x<300 |
| D | 300≤x<400 |
| E | x>400 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为1m,梯子的顶端B到地面的距离为3m,现将梯子的底端A向外移到A′,使梯子的底端A′到墙根O的距离为2m,同时梯子顶端B下降至B′,那么BB′的长( )
如图,梯子AB靠在墙上,梯子的底端A到墙根O的距离为1m,梯子的顶端B到地面的距离为3m,现将梯子的底端A向外移到A′,使梯子的底端A′到墙根O的距离为2m,同时梯子顶端B下降至B′,那么BB′的长( )| A. | 小于1m | B. | 等于1m | C. | 大于1m | D. | 以上都不对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com