
【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE.
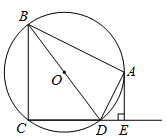
(1)求证:AE是⊙O的切线;
(2)如果AB=4,AE=2,求⊙O的半径.
【答案】
【1】 证明:边结OA,
∵OA=OD,∴∠1=∠2.
∵DA平分![]() ,∴∠2=∠3.
,∴∠2=∠3.
∴∠1=∠3.∴OA∥DE.
∴∠OAE=∠4,[
∵![]() ,∴∠4=90°.∴∠OAE=90°,即OA⊥AE.
,∴∠4=90°.∴∠OAE=90°,即OA⊥AE.
又∵点A在⊙O上,∴AE是⊙O的切线.
【2】 ∵BD是⊙O的直径,∴∠BAD=90°.
∵∠5=90°,∴∠BAD=∠5.
又∵∠2=∠3,∴△BAD∽△AED.∴![]()
∵BA=4,AE=2,∴BD=2AD.
在Rt△BAD中,根据勾股定理,得BD=![]() .
.
∴⊙O半径为![]() .
.
【解析】
试题(1)连接OA,利用已知首先得出OA∥DE,进而证明OA⊥AE就能得到AE是⊙O的切线;
(2)通过证明△BAD∽△AED,再利用对应边成比例关系从而求出⊙O半径的长.
试题解析:(1)连接OA,

∵OA=OD,
∴∠1=∠2.
∵DA平分∠BDE,
∴∠2=∠3.
∴∠1=∠3.∴OA∥DE.
∴∠OAE=∠4,
∵AE⊥CD,∴∠4=90°.
∴∠OAE=90°,即OA⊥AE.
又∵点A在⊙O上,
∴AE是⊙O的切线.
(2)∵BD是⊙O的直径,
∴∠BAD=90°.
∵∠5=90°,∴∠BAD=∠5.
又∵∠2=∠3,∴△BAD∽△AED.
∴![]() ,
,
∵BA=4,AE=2,∴BD=2AD.
在Rt△BAD中,根据勾股定理,
得BD=![]() .
.
∴⊙O半径为![]() .
.


科目:初中数学 来源: 题型:
【题目】某公司购进一批受环境影响较大的商品,需要在特定的环境中才能保存,已知该商品成本y(元/件)与保存的时间第x(天)之间的关系满足y=x2﹣4x+100,该商品售价p(元/件)与保存时间第x(天)之间满足一次函数关系,其对应数据如表:
x(天) | …… | 5 | 7 | …… |
p(元/件) | …… | 248 | 264 | …… |
(1)求商品的售价p(元/件)与保存时间第x(天)之间的函数关系式;
(2)求保存第几天时,该商品不赚也不亏;
(3)请你帮助该公司确定在哪一天卖出,每件商品能获得最大利润,此时每件商品的售价是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
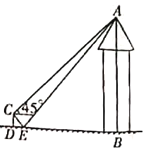
【题目】小亮和小刚利用学过的测量知识测量一座房子的高度,如图所示,他们先在地面上的点![]() 处竖直放了一根标杆
处竖直放了一根标杆![]() ,在房子和标杆之间的地面上平放一平面镜,并在镜面上做了一个标记,小刚来回移动平面镜,当这个标记与地面上的点
,在房子和标杆之间的地面上平放一平面镜,并在镜面上做了一个标记,小刚来回移动平面镜,当这个标记与地面上的点![]() 重合时,小亮在标杆顶端
重合时,小亮在标杆顶端![]() 处刚好看到房子的顶端点
处刚好看到房子的顶端点![]() 在镜面中的像与镜面上的标记重合,此时,在
在镜面中的像与镜面上的标记重合,此时,在![]() 处测得房子顶端点
处测得房子顶端点![]() 的仰角为
的仰角为![]() ,点
,点![]() 到点
到点![]() 的距离为0.8米.标杆
的距离为0.8米.标杆![]() 的长度为1米,已知点
的长度为1米,已知点![]() 在同一水平直线上,且
在同一水平直线上,且![]() 均垂直于
均垂直于![]() ,求房子的高度
,求房子的高度![]() (平面镜的厚度忽略不计)
(平面镜的厚度忽略不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
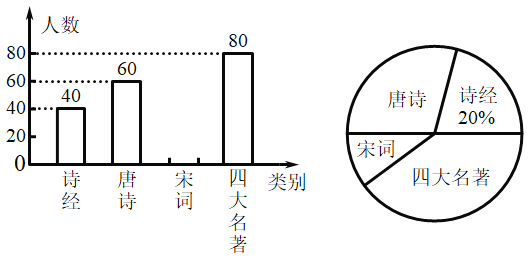
【题目】某校开展诵读“诗经、唐诗、宋词、四大名著”的活动,为了解学生对着四项诵读内容的喜爱程度,在全校学生中随机抽取部分学生进行问卷调查(在这四项诵读内容中,被调查的学生必须满足且只能选择一项)将收集的数据进行整理,并绘制了两幅不完整的统计图(如图)请跟进图中提供的信息,回答以下问题:
(1)本次调查中,随机抽取的学生有__________人,其中喜爱诵读|宋词的有___________人.
(2)补全条形统计图;
(3)若该校有2000名学生,估计全校学生中约有多少人喜爱诵读|宋词?
查看答案和解析>>
科目:初中数学 来源: 题型:
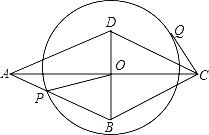
【题目】如图:已知菱形ABCD中,对角线AC和BD相交于点O,AC=8,BD=6,动点P在边AB上运动,以点O为圆心,OP为半径作⊙O,CQ切⊙O于点Q.则在点P运动过程中,切线CQ的长的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图某公园入口有三级台阶,每级台阶高18cm,深30cm,拟将台阶改为斜坡设台阶的起点为A,斜坡的起始点为C,现设计斜坡BC的坡度i=1:5,则AC的长度是( )
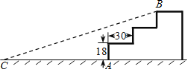
A.270cmB.210cmC.180cmD.96cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,已知
中,已知![]() ,
,![]() ,矩形
,矩形![]() 在直线
在直线![]() 上绕其右下角的顶点
上绕其右下角的顶点![]() 向右旋转90°至图①位置,再绕右下角的顶点继续旋转90°至图②位置,依此类推,这样连续旋转100次后顶点
向右旋转90°至图①位置,再绕右下角的顶点继续旋转90°至图②位置,依此类推,这样连续旋转100次后顶点![]() 在整个旋转过程中所经过的路程之和是_________.
在整个旋转过程中所经过的路程之和是_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某考察船在某海域进行科考活动,在点A测得小岛C在它的东北方向上,它沿南偏东37°方向航行了2海里到达点B处,又测得小岛C在它的北偏东23°方向上.
(1)求∠C的度数;
(2)求该考察船在点B处与小岛C之间的距离.(精确到0.1海里)
(参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,![]() =1.41,
=1.41,![]() =1.73)
=1.73)
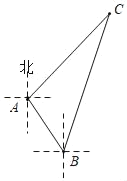
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com