
【题目】某公司购进一批受环境影响较大的商品,需要在特定的环境中才能保存,已知该商品成本y(元/件)与保存的时间第x(天)之间的关系满足y=x2﹣4x+100,该商品售价p(元/件)与保存时间第x(天)之间满足一次函数关系,其对应数据如表:
x(天) | …… | 5 | 7 | …… |
p(元/件) | …… | 248 | 264 | …… |
(1)求商品的售价p(元/件)与保存时间第x(天)之间的函数关系式;
(2)求保存第几天时,该商品不赚也不亏;
(3)请你帮助该公司确定在哪一天卖出,每件商品能获得最大利润,此时每件商品的售价是多少?
【答案】(1)p=8x+208;(2)该商品保存第18天时,不赚也不亏;(3)该商品在第6天卖出时,每件商品能获得最大利润,此时每件商品的售价为256元.
【解析】
(1)设p=kx+b,利用待定系数法求解即可;
(2)根据售价等于成本列出方程并求解即可;
(3)设每件商品所获利润为w元,依题意得w关于x的二次函数,写成顶点式,按照二次函数的性质可得出答案.
(1)设p=kx+b,将x=5,p=248和x=7,p=264分别代入表达式,
得![]()
解得![]()
∴p=8x+208.
(2)依题意,得方程:
8x+208=x2﹣4x+100.
整理方程,得 x2﹣12x﹣108=0.
解得x1=18,x2=﹣6(不合题意,舍去).
答:该商品保存第18天时,不赚也不亏.
(3)设每件商品所获利润为w元,依题意,得:
w=8x+208﹣(x2﹣4x+100)
=﹣x2+12x+108
=﹣(x﹣6)2+144,
∵a=﹣1<0,
∴当x=6时,w最大=144.
∴p=8x+208=8×6+208=256(元).
答:该商品在第6天卖出时,每件商品能获得最大利润,此时每件商品的售价为256元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 为
为![]() 上一点,
上一点,![]() 和过点
和过点![]() 的切线互相垂直,垂足为
的切线互相垂直,垂足为![]() ,
,![]() 交
交![]() 于点
于点![]() ,直线
,直线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
[Failed to download image : http://192.168.0.10:8086/QBM/2020/6/22/2490290299265024/2493010512216064/STEM/6108b9d591da4e268d6d47ef4c154d16.png]
(1)求证:![]() 平分
平分![]() ;
;
(2)探究线段![]() ,
,![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(3)若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情期间,佩戴口罩是做好个人防护的重要举措.小明家先后两次在同一电商平台以相同的单价免邮购买了![]() 、
、![]() 两种型号的口罩.第一次购买20个
两种型号的口罩.第一次购买20个![]() 型口罩,30个
型口罩,30个![]() 型口罩,共花费190元;第二次购买30个
型口罩,共花费190元;第二次购买30个![]() 型口罩,20个
型口罩,20个![]() 型口罩,共花费160元.
型口罩,共花费160元.
(1)求![]() 、
、![]() 两种型号口罩的单价;
两种型号口罩的单价;
(2)“五一”期间,该电商平台举行促销活动,小明发现同样花费160元购买![]() 型口罩,以活动价购买可以比原价多买8个,求“五一”期间
型口罩,以活动价购买可以比原价多买8个,求“五一”期间![]() 型口罩的活动价.
型口罩的活动价.
查看答案和解析>>
科目:初中数学 来源: 题型:
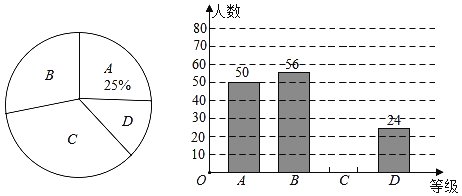
【题目】《中国诗词大会》是央视首档全民参与的诗词节目,节目以“赏中华诗词、寻文化基因、品生活之美”为基本宗旨,力求通过对诗词知识的比拼及赏析,带动全民重温那些曾经学过的古诗词,分享诗词之美,感受诗词之趣,从古人的智慧和情怀中汲取营养,涵养心灵.我市某中学举办了网上诗词大赛,大赛的成绩分为四个等级:优秀、良好、及格、不及格(分别用A,B,C,D表示).为了了解该校学生对诗词的掌握程度,赛后随机抽取了部分学生的成绩进行整理,并将结果绘制了如下两幅不完整的统计图.
(1)本次抽取的学生共有 人,扇形统计图中不及格学生所占的圆心角的度数为 .
(2)请根据计算补全条形统计图;
(3)若某校有1200名学生,请你根据调查结果估计该校学生诗词大赛成绩为“优秀”和“良好”两个等级共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
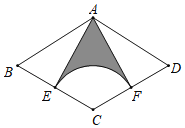
【题目】如图,在菱形ABCD中,点E是BC的中点,以C为圆心,CE为半径作弧,交CD于点F,连接AE、AF.若AB=6,∠B=60°,则阴影部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C(0,3),且抛物线的顶点坐标为(1,4).
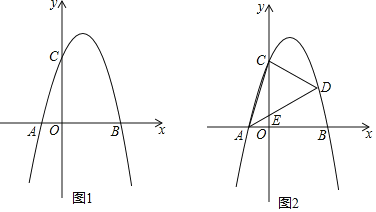
(1)求抛物线的解析式;
(2)如图2,点D是第一象限抛物线上的一点,AD交y轴于点E,设点D的横坐标为m,设△CDE的面积为S,求S与m的函数关系式(不必写出自变量的取值范围);
(3)在(2)的条件下,连接AC,是否存在这样的点D,使得∠DAB=2∠ACO,若存在,求点D的坐标及相应的S的值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象经过点
的图象经过点![]() ,
,![]() ,且与y轴交于点C.
,且与y轴交于点C.
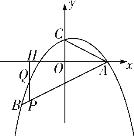
(1)求二次函数的解析式;
(2)证明:![]() (其中O是原点);
(其中O是原点);
(3)若P是线段![]() 上的一个动点(不与A、B重合),过点P作y轴的平行线,分别交此二次函数图象及x轴于Q、H两点,试问:是否存在这样的点P,使
上的一个动点(不与A、B重合),过点P作y轴的平行线,分别交此二次函数图象及x轴于Q、H两点,试问:是否存在这样的点P,使![]() ?若存在,请求出点P的坐标;若不存在,请说明理由.
?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,BD是⊙O的直径,AE⊥CD于点E,DA平分∠BDE.
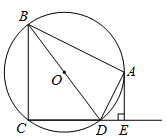
(1)求证:AE是⊙O的切线;
(2)如果AB=4,AE=2,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com