【题目】如图，在矩形
中，
于
，
，
，则
的面积是（ ）
A. 
B. 
C. 
D. 
【答案】C
【解析】
过点C作CF⊥BD于F，根据矩形的性质可得AE=CF，利用勾股定理列式求出BD，然后利用△ABD的面积列式求出AE，再根据勾股定理求出DE，然后利用三角形的面积列式计算即可得解．
过点C作CF⊥BD于F．
∵AE⊥BD，∴∠AEB=∠CFD=90°．
∵ABCD是矩形，∴AB=CD，AB∥DC，∴∠ABD=∠CDF，∴△ABE≌△CDF，∴AE=CF，在矩形ABCD中，AD=BC=3，∠BAD=90°，由勾股定理得：BD=
=
=2
．
∵AE⊥BD，∴S△ABD=
×2AE=×3×，解得：AE=
．在Rt△AED中，由勾股定理得：DE=
=
，所以，△DEC的面积=××=
．
故选C．
夺冠金卷全能练考系列答案科目：初中数学 来源： 题型：
【题目】如图，△ABC中，∠ACB=90°，AD平分∠BAC，DE⊥AB于E．
（1）若∠BAC=50°，求∠EDA的度数；
（2）求证：直线AD是线段CE的垂直平分线．
查看答案和解析>>
科目：初中数学 来源： 题型：
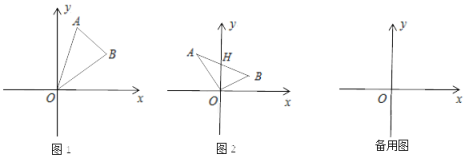
【题目】在平面直角坐标系中，O为坐标原点，A(m,n+1),B(m+2,n).
（1）当m=1,n=2时.如图1，连接AB、AO、BO.直接写出△ABO的面积为 .
（2）如图2，若点A在第二象限、点B在第一象限，连接AB、AO、BO,AB交y轴于H，△ABO的面积为2.求点H的坐标.
（3）若点A、B在第一象限，在y 轴正半轴上存在点C，使得∠CAB=900,且CA=AB,求m的值，及OC的长（用含n的式子表示）.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“丹棱冻粑”是眉山著名特色小吃，产品畅销省内外，现有一个产品销售点在经销时发现：如果每箱产品盈利10元，每天可售出50箱；若每箱产品涨价1元，日销售量将减少2箱．
（1）现该销售点每天盈利600元，同时又要顾客得到实惠，那么每箱产品应涨价多少元？
（2）若该销售点单纯从经济角度考虑，每箱产品应涨价多少元才能获利最高？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在四边形ABCD中，AD∥BC，E是AB的中点，连接DE并延长交CB的延长线于点F，点M在BC边上，且∠MDF=∠ADF。
（1）求证：△ADE≌△BFE；
（2）如果FM=CM，求证：EM垂直平分DF．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列材料，并完成任务。
筝形的定义:两组邻边分别相等的四边形叫做筝形，几何图形的定义通常可作为图形的性质也可以作为图形的判定方法.也就是说，如图，若四边形ABCD是一个筝形，则AB=AD，BC=CD；若AB=AD，BC=CD，则四边形ABCD是筝形.
如图，四边形ABCD是一个筝形，其中AB=AD，BC=CD.对角线AC，BD相交于点O，过点0作0M⊥AB，ON⊥AD，垂足分别为M，N.求证:四边形AMON是筝形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
