
分析 (1)当x>120时,此时每件涨价(x-120)元,少卖10(x-120)件,实际卖出[300-10(x-120)]件,列出函数解析式,求得最大值即可;
(2)当110≤x<120时,此时每件降价(120-x)元,多卖20(120-x)件,实际卖出[300+20(120-x)]件,由利润=(售价-进价)×卖的件数,列出关系式,把二次函数解析式写成顶点坐标式,求出最大值即可.
解答 解:设商店应将该商品定价为x元,利润为W,
(1)由题意得W=(x-100)[300-10(x-120)]=-10x2+2500x-150000=-10(x-125)2+6250,
当为了获得最大利润,商店应将该商品定价为125元;
(2)由题意得:
W=(x-100)[300+20(120-x)]=-20x2+4700x-270000=-20(x-117.5)2+6125,
∵售价为整数,
∴当x=117或118时,获利最大利润,
又∵能更好地清库存,
∴当定价为118元时,利润最大为6120元.
点评 此题主要考查了二次函数的性质在实际生活中的应用,最大销售利润的问题常利函数的增减性来解答,要注意应该在自变量的取值范围内求最大值(或最小值),也就是说二次函数的最值在x=-$\frac{b}{2a}$时取得.


科目:初中数学 来源: 题型:选择题
| A. | ①②③④ | B. | ①④②③ | C. | ①④③② | D. | ②①④③ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
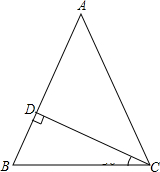 已知:如图,△ABC中,AB=AC,CD⊥AB于点D.求证:∠BAC=2∠DCB.(温馨提示:要用到三线合一的性质哟!聪明的你想到了吗?)
已知:如图,△ABC中,AB=AC,CD⊥AB于点D.求证:∠BAC=2∠DCB.(温馨提示:要用到三线合一的性质哟!聪明的你想到了吗?)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com