
【题目】如图1,点A坐标为(2,0),以OA为边在第一象限内作等边△OAB,点C为x轴上一动点,且在点A右侧,连接BC,以BC为边在第一象限内作等边△BCD,连接AD交BC于E.
(1)①直接回答:△OBC与△ABD全等吗?
②试说明:无论点C如何移动,AD始终与OB平行;
(2)当点C运动到使AC2=AEAD时,如图2,经过O、B、C三点的抛物线为y1 . 试问:y1上是否存在动点P,使△BEP为直角三角形且BE为直角边?若存在,求出点P坐标;若不存在,说明理由;
(3)在(2)的条件下,将y1沿x轴翻折得y2 , 设y1与y2组成的图形为M,函数y= ![]() x+
x+ ![]() m的图象l与M有公共点.试写出:l与M的公共点为3个时,m的取值.
m的图象l与M有公共点.试写出:l与M的公共点为3个时,m的取值.
【答案】
(1)
解:①△OBC与△ABD全等,
理由是:如图1,∵△OAB和△BCD是等边三角形,
∴∠OBA=∠CBD=60°,
OB=AB,BC=BD,
∴∠OBA+∠ABC=∠CBD+∠ABC,
即∠OBC=∠ABD,
∴△OBC≌△ABD(SAS);
②∵△OBC≌△ABD,
∴∠BAD=∠BOC=60°,
∴∠OBA=∠BAD,
∴OB∥AD,
∴无论点C如何移动,AD始终与OB平行

(2)
解:如图2,

∵AC2=AEAD,
∴ ![]() ,
,
∵∠EAC=∠DAC,
∴△AEC∽△ACD,
∴∠ECA=∠ADC,
∵∠BAD=∠BAO=60°,
∴∠DAC=60°,
∵∠BED=∠AEC,
∴∠ACB=∠ADB,
∴∠ADB=∠ADC,
∵BD=CD,
∴DE⊥BC,
Rt△ABE中,∠BAE=60°,
∴∠ABE=30°,
∴AE= ![]() AB=
AB= ![]() ×2=1,
×2=1,
Rt△AEC中,∠EAC=60°,
∴∠ECA=30°,
∴AC=2AE=2,
∴C(4,0),
等边△OAB中,过B作BH⊥x轴于H,
∴BH= ![]() =
= ![]() ,
,
∴B(1, ![]() ),
),
设y1的解析式为:y=ax(x﹣4),
把B(1, ![]() )代入得:
)代入得: ![]() =a(1﹣4),
=a(1﹣4),
a=﹣ ![]() ,
,
∴设y1的解析式为:y1=﹣ ![]() x(x﹣4)=﹣
x(x﹣4)=﹣ ![]() x2+
x2+ ![]() x,
x,
过E作EG⊥x轴于G,
Rt△AGE中,AE=1,
∴AG= ![]() AE=
AE= ![]() ,
,
EG= ![]() =
= ![]() ,
,
∴E( ![]() ,
, ![]() ),
),
设直线AE的解析式为:y=kx+b,
把A(2,0)和E( ![]() ,
, ![]() )代入得:
)代入得: 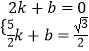 ,
,
解得: ![]() ,
,
∴直线AE的解析式为:y= ![]() x﹣2
x﹣2 ![]() ,
,
则  ,
,
解得: ![]() ,
, ![]() ,
,
∴P(3, ![]() )或(﹣2,﹣4
)或(﹣2,﹣4 ![]() )
)
(3)
解:如图3,

y1=﹣ ![]() x2+
x2+ ![]() x=﹣
x=﹣ ![]() (x﹣2)2+
(x﹣2)2+ ![]() ,
,
顶点(2, ![]() ),
),
∴抛物线y2的顶点为(2,﹣ ![]() ),
),
∴y2= ![]() (x﹣2)2﹣
(x﹣2)2﹣ ![]() ,
,
当m=0时,y= ![]() x与图形M两公共点,
x与图形M两公共点,
当y2与l相切时,即有一个公共点,l与图形M有3个公共点,
则  ,
,
![]() =
= ![]() ﹣
﹣ ![]() ,
,
x2﹣7x﹣3m=0,
△=(﹣7)2﹣4×1×(﹣3m)≥0,
m≥﹣ ![]() ,
,
∴当l与M的公共点为3个时,m的取值是:﹣ ![]() ≤m<0.
≤m<0.
【解析】(1)①利用等边三角形的性质证明△OBC≌△ABD;②证明∠OBA=∠BAD=60°,可得OB∥AD;(2)首先证明DE⊥BC,再求直线AE与抛物线的交点就是点P,所以分别求直线AE和抛物线y1的解析式组成方程组,求解即可;(3)先画出如图3,根据图形画出直线与图形M有个公共点时,两个边界的直线,上方到y= ![]() x,将y=
x,将y= ![]() x向下平移即可满足l与图形M有3个公共点,一直到直线l与y2相切为止,主要计算相切时,列方程组,确定△≥0时,m的值即可.
x向下平移即可满足l与图形M有3个公共点,一直到直线l与y2相切为止,主要计算相切时,列方程组,确定△≥0时,m的值即可.
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法,以及对等边三角形的性质的理解,了解等边三角形的三个角都相等并且每个角都是60°.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E为AB边上一点,EC平分∠DEB,F为CE的中点,连接AF,BF,过点E作EH∥BC分别交AF,CD于G,H两点. 
(1)求证:DE=DC;
(2)求证:AF⊥BF;
(3)当AFGF=28时,请直接写出CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数y= ![]() (k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.
(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.
(1)求这个反比函数的解析式;
(2)求△ACD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如下,则一次函数y=ax﹣2b与反比例函数y= ![]() 在同一平面直角坐标系中的图象大致是( )
在同一平面直角坐标系中的图象大致是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点O是边AC上一个动点,过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E、F.
(1)若CE=8,CF=6,求OC的长;
(2)连接AE、AF.问:当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一座钢结构桥梁的框架是△ABC,水平横梁BC长18米,中柱AD高6米,其中D是BC的中点,且AD⊥BC. 
(1)求sinB的值;
(2)现需要加装支架DE、EF,其中点E在AB上,BE=2AE,且EF⊥BC,垂足为点F,求支架DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为5,点A的坐标为(﹣4,0),点B在y轴上,若反比例函数y= ![]() (k≠0)的图象过点C,则该反比例函数的表达式为( )
(k≠0)的图象过点C,则该反比例函数的表达式为( ) 
A.y= ![]()
B.y= ![]()
C.y= ![]()
D.y= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,点E,O,F分别为AB,AC,AD的中点,连接CE,CF,OE,OF. 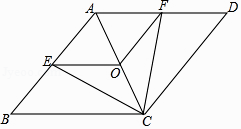
(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么关系时,四边形AEOF是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游乐场部分平面图如图所示,C、E、A在同一直线上,D、E、B在同一直线上,测得A处与E处的距离为80 米,C处与D处的距离为34米,∠C=90°,∠BAE=30°.( ![]() ≈1.4,
≈1.4, ![]() ≈1.7)
≈1.7) 
(1)求旋转木马E处到出口B处的距离;
(2)求海洋球D处到出口B处的距离(结果保留整数).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com