
小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
| 月均用水量(单位:t) | 频数 |
|
|
| 2 | 4% |
|
| 12 | 24% |
|
| ||
|
| 10 | 20% |
|
| 12% | |
|
| 3 | 6% |
|
| 2 | 4% |
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
(2)如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户?
(3)从月均用水量在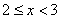 ,
,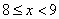 这两个范围内的样本家庭中任意抽取2个,求抽取出的2个家庭来自不同范围的概率.
这两个范围内的样本家庭中任意抽取2个,求抽取出的2个家庭来自不同范围的概率.
解:(1)∵月均用水量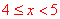 所占百分比为
所占百分比为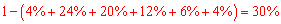 ;
;
月均用水量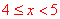 的频数为
的频数为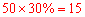 ;月均用水量
;月均用水量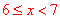 的频数为
的频数为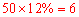 ,
,
∴补全频数分布表和频数分布直方图如下:
| 月均用水量(单位:t) | 频数 |
|
|
| 2 | 4% |
|
| 12 | 24% |
|
| 15 | 30% |
|
| 10 | 20% |
|
| 6 | 12% |
|
| 3 | 6% |
|
| 2 | 4% |
(2)∵样本中家庭月均用水量“大于或等于4t且小于7t”占62%,
∴估计总体中的中等用水量家庭大约有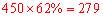 (户).
(户).
(3)设月均用水量在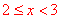 范围内的样本家庭为
范围内的样本家庭为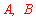 ,月均用水量在
,月均用水量在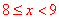 范围内的样本家庭为
范围内的样本家庭为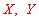 ,
,
∵从月均用水量在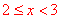 ,
,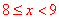 这两个范围内的样本家庭中任意抽取2个,共有6种等可能结果:
这两个范围内的样本家庭中任意抽取2个,共有6种等可能结果: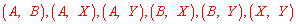 ,抽取出的2个家庭来自不同范围的有4种情况:
,抽取出的2个家庭来自不同范围的有4种情况: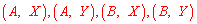 ,
,
∴抽取出的2个家庭来自不同范围的概率为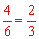 .为
.为
【考点】频数分布表和频数分布直方图;频数、频率和总量的关系;用样本估计总体;概率.
【分析】(1)由已知信息,根据频数、频率和总量的关系,求出月均用水量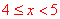 所占百分比和频数,月均用水量
所占百分比和频数,月均用水量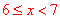 的频数,从而补全频数分布表和频数分布直方图.
的频数,从而补全频数分布表和频数分布直方图.
(2)求出样本中家庭月均用水量“大于或等于4t且小于7t” 所占百分比,即可用样本估计总体.
(3)根据概率的求法,找准两点:①全部等可能情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
玉龙工艺品商场按标价销售某种工艺品时,每件可获利45元;按标价的八五折
销售该工艺品8件与将标价降低35元销售该工艺品12件所获利润相等.
(1)该工艺品每件的进价、标价分别是多少元?
(2)若每件工艺品按(1)中求得的进价进货,标价售出,工艺商场每天可售
出该工艺品100件.若每件工艺品降价1元,则每天可多售出该工艺品4件.问
现在进行适当降价活动,且降价不超过8元,问每件工艺品降价多少元出售,
每天获 得的利润最大?获得的最大利润是多少元?
得的利润最大?获得的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
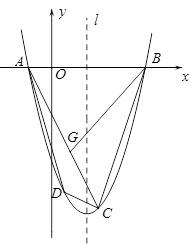
如图,已知二次函数的图象M经过A(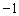 ,0),B(4,0),C(2,
,0),B(4,0),C(2,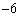 )三点.
)三点.
(1)求该二次函数的解析式;
(2)点G是线段AC上的动点(点G与线段AC的端点不重合),若△ABG与△ABC相似,求点G的坐标
(3)设图象M的对称轴为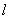 ,点
,点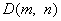
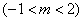 是图象M上一动点,当△ACD的面积为
是图象M上一动点,当△ACD的面积为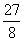 时,点D关于
时,点D关于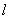 的对称点为E,能否在图象M和
的对称点为E,能否在图象M和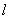 上分别找到点P、Q,使得以点D、E、P、Q为顶点的四边形为平行四边形. 若能,求出点P的坐标;若不能,请说明理由.
上分别找到点P、Q,使得以点D、E、P、Q为顶点的四边形为平行四边形. 若能,求出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
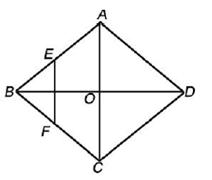
如图,菱形ABCD的对角线AC、BC相交于点O,E、F分别是AB、BC边上的中点,连接EF,若
EF=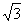 ,BD=4,则菱形ABCD的周长为( ).
,BD=4,则菱形ABCD的周长为( ).
A.4 B. C.
C.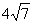 D.28
D.28
查看答案和解析>>
科目:初中数学 来源: 题型:
问题提出:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
问题探究:不妨假设能搭成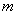 种不同的等腰三角形,为探究
种不同的等腰三角形,为探究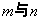 之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
探究一:
(1)用3根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
此时,显然能搭成一种等腰三角形。所以,当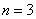 时,
时,
(2)用4根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形
所以,当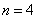 时,
时,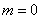
(3)用5根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形
所以,当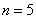 时,
时,
(4)用6根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形
所以,当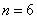 时,
时,
综上所述,可得表①
|
| 3 | 4 | 5 | 6 |
|
| 1 | 0 | 1 | 1 |
探究二:
(1)用7根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(仿照上述探究方法,写出解答过程,并把结果填在表②中)
(2) 分别用8根、9根、10根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(只需把结果填在表②中)
|
| 7 | 8 | 9 | 10 |
|
|
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,……
解决问题:用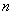 根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
(设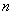 分别等于
分别等于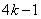 、
、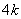 、
、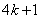 、
、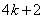 ,其中
,其中 是整数,把结果填在表③中)
是整数,把结果填在表③中)
|
|
|
|
|
|
|
|
问题应用:用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
(要求写出解答过程)
其中面积最大的等腰三角形每个腰用了__________________根木棒。(只填结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com