
ЁОЬтФПЁПШчЭМЃЌжБЯпABНЛxжсгкЕуAЃЈaЃЌ0ЃЉЃЌНЛyжсгкЕуBЃЈ0ЃЌbЃЉЃЌЧвaЁЂbТњзу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЕуAЕФзјБъЮЊ ЃЛЕуBЕФзјБъЮЊ ЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌШєЕуCЕФзјБъЮЊЃЈЃ3ЃЌЃ2ЃЉЃЌЧвBEЁЭACгкЕуEЃЌODЁЭOCНЛBEбгГЄЯпгкDЃЌЪдЧѓЕуDЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌMЁЂNЗжБ№ЮЊOAЁЂOBБпЩЯЕФЕуЃЌOM=ONЃЌOPЁЭANНЛABгкЕуPЃЌЙ§ЕуP зїPGЁЭBMЃЌНЛANЕФбгГЄЯпгкЕуGЃЌЧыаДГіЯпЖЮAGЁЂOPгыPGжЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУїФуЕФНсТлЃЎ

ЁОД№АИЁПЃЈ1ЃЉ A(5ЃЌ0) ЃЌB(0ЃЌ-5) ЃЛЃЈ2ЃЉD(2ЃЌ3)ЃЛ(3) OP+PG=AGЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнЗЧИКЪ§ЕФаджЪЕУГіa=5ЃЌb=Љ5МДПЩЃЛ
ЃЈ2ЃЉЙ§CзїCKЁЭxжсЃЌЙ§DзїCFЁЭyжсЃЌдйРћгУAASжЄУїЁїAOCгыЁїDOBШЋЕШМДПЩЃЛ
ЃЈ3ЃЉбгГЄGPЕНLЪЙPL=OPЃЌСЌНгALЃЌжЄУїЁїPALгыЁїOAPШЋЕШЃЌдйРћгУШЋЕШШ§НЧаЮЕФаджЪНтД№МДПЩЃЎ
ЪдЬтНтЮіЃКНтЃКЃЈ1ЃЉЁп|a+b|+ЃЈaЉ5ЃЉ2=0ЃЌЁрa=5ЃЌb=Љ5ЃЌЁрЕуAЕФзјБъЮЊЃЈ5ЃЌ0ЃЉЃЌЕуBЕФзјБъЮЊЃЈ0ЃЌЉ5ЃЉЃЌЙЪД№АИЮЊЃКЃЈ5ЃЌ0ЃЉЃЛЃЈ0ЃЌЉ5ЃЉЃЛ
ЃЈ2ЃЉЙ§CзїCKЁЭxжсЃЌЙ§DзїDFЁЭyжсЃЌЁпЁЯAED=ЁЯBOK=90ЁуЃЌЁрЁЯDBO=ЁЯOACЃЌЁпЁЯAOB+BOC=ЁЯBOK+ЁЯBOC=90Ёу+ЁЯBOCЃЌЁрЁЯAOC=ЁЯBODЃЌдкЁїAOCгыЁїDOBжаЃЌЁпЁЯAOC=ЁЯBODЃЌЁЯDBO=ЁЯOACЃЌOA=OBЃЌЁрЁїAOCЁеЁїDOBЃЈAASЃЉЃЌЁрOC=ODЃЌдкЁїOCKгыЁїODFжаЃЌЁпЁЯDFO=ЁЯCKO=90ЁуЃЌЁЯDOF=ЁЯCOKЃЌOD=OCЃЌЁрЁїOCKЁеЁїODFЃЌЁрDF=CKЃЌOK=OFЃЌЁрDЃЈЉ2ЃЌ3ЃЉЃЛ
ЃЈ3ЃЉбгГЄGPЕНLЃЌЪЙPL=OPЃЌСЌНгALЃЌдкЁїAONгыЁїBOMжаЃЌЁпON=OMЃЌЁЯAON=ЁЯBOMЃЌOA=OBЃЌЁрЁїAONЁеЁїBOMЃЌЁрЁЯOAN=ЁЯOBMЃЌЁрЁЯMBA=ЁЯNABЃЌЁпPGЁЭBMЃЌOPЁЭANЃЌЁрЁЯNAB+ЁЯOPA=ЁЯMBA+ЁЯGPB=90ЁуЃЌЁрЁЯOPA=ЁЯGPB=ЁЯAPLЃЌдкЁїOAPгыЁїPALжаЃЌЁпPL=OPЃЌЁЯAPL=ЁЯOPAЃЌAP=APЃЌЁрЁїOAPЁеЁїPALЃЌЁрЁЯPOA=ЁЯLЃЌЁЯOAP=ЁЯPAL=45ЁуЃЌЁрЁЯOAL=90ЁуЃЌЁрЁЯPOA=90ЁуЉЁЯPOBЃЌЁЯGAL=90ЁуЉЁЯOANЃЌЁпЁЯPOB=ЁЯOANЃЌЁрЁЯPOA=ЁЯGOLЃЌЁрЁЯPOA=ЁЯGOL=ЁЯLЃЌЁрAG=GLЃЌЁрAG=GL=GP+PL=GP+OPЃЎ



 ЕМбЇШЋГЬСЗДДгХбЕСЗЯЕСаД№АИ
ЕМбЇШЋГЬСЗДДгХбЕСЗЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуAЁЂFЁЂCЁЂDдкЭЌвЛЬѕжБЯпЩЯЃЌвбжЊAF=DCЃЌЁЯA=ЁЯDЃЌBCЁЮEFЃЌЧѓжЄЃКAB=DEЃЎ

ЁОД№АИЁПжЄУїМћНтЮіЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКгћжЄУїAB=DEЃЌжЛвЊжЄУїЁїABCЁеЁїDEFМДПЩЃЎ
ЪдЬтНтЮіЃКЁпAF=CDЃЌ
ЁрAC=DFЃЌ
ЁпBCЁЮEFЃЌ
ЁрЁЯACB=ЁЯDFEЃЌ
дкЁїABCКЭЁїDEFжаЃЌ
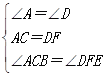 ЃЌ
ЃЌ
ЁрЁїABCЁеЁїDEFЃЈASAЃЉЃЌ
ЁрAB=DEЃЎ
ПМЕуЃКШЋЕШШ§НЧаЮЕФХаЖЈгыаджЪЃЎ
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
25
ЁОЬтФПЁПШчЭМЃЌ ![]() ЃЌAE=BDЃЌЕуDдкACБпЩЯЃЌ
ЃЌAE=BDЃЌЕуDдкACБпЩЯЃЌ ![]() ЃЌAEКЭBDЯрНЛгкЕуOЃЎ
ЃЌAEКЭBDЯрНЛгкЕуOЃЎ

ЃЈ1ЃЉЧѓжЄЃКЁїAECЁеЁїBEDЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓBDEЕФЖШЪ§ЃЎ
ЃЌЧѓBDEЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
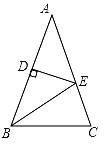
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌAB=ACЃЌDЪЧABЕФжаЕуЃЌЧвDEЁЭABЃЌЁїBCEЕФжмГЄЮЊ8cmЃЌЧвACЉBC=2cmЃЌЧѓABЁЂBCЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
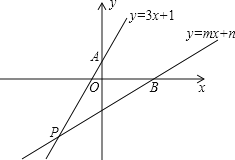
ЁОЬтФПЁПШчЭМЃЌвбжЊжБЯп![]() ЃКy=3x+1гыyжсНЛгкЕуAЃЌЧвКЭжБЯп
ЃКy=3x+1гыyжсНЛгкЕуAЃЌЧвКЭжБЯп![]() ЃКy=mx+nНЛгкЕуPЃЈ-2ЃЌaЃЉЃЌИљОнвдЩЯаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃКy=mx+nНЛгкЕуPЃЈ-2ЃЌaЃЉЃЌИљОнвдЩЯаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧѓaЕФжЕЃЌХаЖЯжБЯп![]() ЃКy=Ѓ
ЃКy=Ѓ![]() x-2ЪЧЗёвВОЙ§ЕуPЃПЧыЫЕУїРэгЩЃЛ
x-2ЪЧЗёвВОЙ§ЕуPЃПЧыЫЕУїРэгЩЃЛ
ЃЈ2ЃЉВЛНтЙигкxЃЌyЕФЗНГЬзщ![]() ЃЌЧыФужБНгаДГіЫќЕФНтЃЛ
ЃЌЧыФужБНгаДГіЫќЕФНтЃЛ
ЃЈ3ЃЉШєЕуBЕФзјБъЮЊЃЈ3,0ЃЉЃЌСЌНгABЃЌЧѓ![]() ЕФУцЛ§.
ЕФУцЛ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=ax2+bx+cЮЊxжсЕФвЛНЛЕуЮЊAЃЈЉ6ЃЌ0ЃЉЃЌгыyжсЕФНЛЕуЮЊCЃЈ0ЃЌ3ЃЉЃЌЧвОЙ§ЕуGЃЈЉ2ЃЌ3ЃЉЃЎ

(1)ЧѓХзЮяЯпЕФБэДяЪН.
(2)ЕуPЪЧЯпЖЮOAЩЯвЛЖЏЕуЃЌЙ§PзїЦНаагкyжсЕФжБЯпгыACНЛгкЕуQЃЌЩшЁїCPQЕФУцЛ§ЮЊSЃЌЧѓSЕФзюДѓжЕ.
(3)ШєЕуBЪЧХзЮяЯпгыxжсЕФСэвЛЖЈЕуЃЌЕуDЁЂMдкЯпЖЮABЩЯЃЌЕуNдкЯпЖЮACЩЯЃЌЁЯDCB=ЁЯCDBЃЌCDЪЧMNЕФДЙжБЦНЗжЯпЃЌЧѓЕуMЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуCЪЧЯпЖЮABЩЯвЛЕуЃЌЁїACDКЭЁїBCEЖМЪЧЕШБпШ§НЧаЮЃЌСЌНсAEЃЌBDЃЌЩшAEНЛCDгкЕуFЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїACEЁеЁїDCBЃЛ
ЃЈ2ЃЉЧѓжЄЃКЁїADFЁзЁїBADЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЕуPдкЕкЖўЯѓЯоЃЌPЕНxжсЕФОрРыЪЧ2ЃЌЕНyжсЕФОрРыЪЧ3ЃЌPЕФзјБъЮЊ___________ЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжБРтжљЕФВрУцЖМЪЧЃЈ ЃЉ
A.е§ЗНаЮ
B.ГЄЗНаЮ
C.ЮхБпаЮ
D.СтаЮ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГбЇЯАаЁзщ13УћбЇЩњЕФвЛДЮгЂгяЬ§СІВтЪдГЩМЈЗжВМШчЯТБэЫљЪОЃЈТњЗж20ЗжЃЉЃК
ГЩМЈЃЈЗжЃЉ | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
ШЫЪ§ЃЈШЫЃЉ | 1 | 3 | 2 | 2 | 1 | 2 | 2 |
ет13УћбЇЩњЬ§СІВтЪдГЩМЈЕФжаЮЛЪ§ЪЧЃЈ ЃЉ
A.16Зж
B.17Зж
C.18Зж
D.19Зж
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com