
好学的小宸利用电脑作了如下的探索:
(1)如图①,将边长为2的等边三角形复制若干个后向右平移,使一条边在同一直线上.则△A2C1B1的面积为 ;
(2)求△A4C3B3的面积;
(3)在保持图①中各三角形的边OB1=B1B2=B2B3=B3B4=2不变的前提下,小宸又作了如下探究:将顶点A1、A2、A3、A4向上平移至同一高度(如图②),若OA4=OB4,试判断以OA2、OA3和OA4为三边能否构成三角形?若能,请判断这个三角形的形状;若不能,请说明理由.

(1)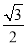 ;(2)
;(2)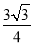 .(3)这三边能构成直角三角形.
.(3)这三边能构成直角三角形.
【解析】
试题分析:(1)分别过A2、C1作x轴的垂线,垂足分别为E、F,根据勾股定理求得相应线段的长度,由△A2C1B1=S梯形A1EFC1-△C1FB1-△A2EB1可求得;
(2)分别计算△A4B3B4、△A4OB4的面积,利用相似三角形即可求出△A4C3B3的面积;
(3)根据勾股定理的逆定理即可判定三角形为直角三角形.
试题解析:(1) 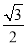 ;
;
(2)解得△A4B3B4的面积为:
解得△A4OB4的面积为: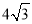
利用△OC3B3∽△OA4B4得:S四边形C3B3B4A4:S△OA4B4=7:16
∴四边形C3B3B4A4的面积为: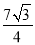
∴△A4C3B3的面积为: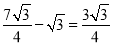 .
.
(3)能.
设这些等腰三角形的高为h.
则:OA22=9+h2,
OA32=25+h2,
OA42=64
∵OA4=OB4
∴∠OA4B=∠OB4A4=∠A4B3B4
∴△OA4B4∽△A4B4B3
∴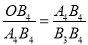
∴A4B4=4
∴h2=15
∴OA22+OA32=OA42
即这三边能构成直角三角形.
考点:1.相似三角形的判定与性质;2.直角三角形的判定.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2013-2014学年江苏省常州市九年级中考一模数学试卷(解析版) 题型:填空题
如图,在3×3的正方形网格中,已有两个小正方形被涂黑,再将图中剩余的编号为1~7的小正方形中任意一个涂黑,则所得图案是一个轴对称图形的概率是 .

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省宜兴市和桥学区九年级下学期期中考试(一模)数学试卷(解析版) 题型:选择题
下列图形中,既是中心对称图形又是轴对称图形的是 ( )

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省太仓市九年级5月学科教学质量调研数学试卷(解析版) 题型:解答题
如图,在□ABCD中,BC=2AB=4,点E、F分别是BC、AD的中点.
(1)求证:△ABF≌△CDF;
(2)当四边形AECF为菱形时,求□ABCD的面积.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省太仓市九年级5月学科教学质量调研数学试卷(解析版) 题型:填空题
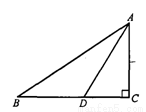
如图,在Rt△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,CD=2,则点D到AB的距离是 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省句容市九年级下学期期中考试(即一模)数学试卷(解析版) 题型:解答题
函数 和
和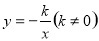 的图象关于y轴对称,我们定义函数
的图象关于y轴对称,我们定义函数 和
和 相互为“影像”函数。
相互为“影像”函数。
类似地,如果函数 和
和 的图象关于y轴对称,那么我们定义函数
的图象关于y轴对称,那么我们定义函数 和
和 互为“影像”函数。
互为“影像”函数。
(1)请写出函数 的“影像”函数: ;
的“影像”函数: ;
(2)函数 的“影像”函数是 ;
;
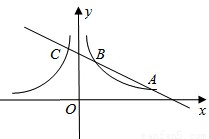
(3)如果,一条直线与一对“影像”函数 和
和 的图象分别交于点A、B、C(点A、B在第一象限),如果CB: BA=1:2,点C在函数
的图象分别交于点A、B、C(点A、B在第一象限),如果CB: BA=1:2,点C在函数 的“影像”函数上的对应点的横坐标是1,求点B的坐标。
的“影像”函数上的对应点的横坐标是1,求点B的坐标。
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省南京市溧水区中考一模数学试卷(解析版) 题型:填空题
如图,在△ABC中,AB=AC,∠A=36°,AB的垂直平分线交AC点E,垂足为点D,连接BE,则∠EBC的度数为 °.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com