
如图,在□ABCD中,BC=2AB=4,点E、F分别是BC、AD的中点.
(1)求证:△ABF≌△CDF;
(2)当四边形AECF为菱形时,求□ABCD的面积.

(1).证明见解析;(2). 2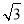 .
.
【解析】
试题分析:第(1)问要证明三角形全等,由平行四边形的性质,很容易用SAS证全等.
第(2)要求菱形的面积,在第(1)问的基础上很快知道△ABE为等边三角形.这样菱形的高就可求了,用面积公式可求得.
试题解析:(1)证明:∵在?ABCD中,AB=CD,
∴BC=AD,∠ABC=∠CDA.
又∵BE=EC= BC,AF=DF=
BC,AF=DF= AD,
AD,
∴BE=DF.
∴△ABE≌△CDF.
(2)【解析】
∵四边形AECF为菱形时,
∴AE=EC.
又∵点E是边BC的中点,
∴BE=EC,即BE=AE.
又BC=2AB=4,
∴AB= BC=BE,
BC=BE,
∴AB=BE=AE,即△ABE为等边三角形,
?ABCD的BC边上的高为2×sin60°=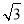
∴菱形AECF的面积为2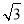 .
.
考点:1.菱形的性质;2.全等三角形的判定;3.平行四边形的性质.


科目:初中数学 来源:2013-2014学年江苏省九年级新课结束考试数学试卷(解析版) 题型:解答题
如图,在直角坐标系xOy中,直线 与双曲线
与双曲线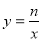 相交于
相交于 、B
、B 两点,矩形
两点,矩形 的边
的边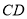 恰好被点
恰好被点 平分,边
平分,边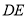 交双曲线于
交双曲线于 点,四边形
点,四边形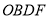 的面积为2.
的面积为2.

(1)求n的值;
(2)求不等式 的解集
的解集
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省九年级新课结束考试数学试卷(解析版) 题型:选择题
如图,△ 中,
中, ∥
∥ ,
, :
: =1:2,则△
=1:2,则△ 与四边形
与四边形 的面积之比是( )
的面积之比是( )
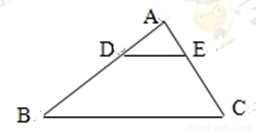
A.1:4 B.1:8 C.1:3 D.1:7
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省太仓市九年级5月学科教学质量调研数学试卷(解析版) 题型:解答题
好学的小宸利用电脑作了如下的探索:
(1)如图①,将边长为2的等边三角形复制若干个后向右平移,使一条边在同一直线上.则△A2C1B1的面积为 ;
(2)求△A4C3B3的面积;
(3)在保持图①中各三角形的边OB1=B1B2=B2B3=B3B4=2不变的前提下,小宸又作了如下探究:将顶点A1、A2、A3、A4向上平移至同一高度(如图②),若OA4=OB4,试判断以OA2、OA3和OA4为三边能否构成三角形?若能,请判断这个三角形的形状;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省太仓市九年级5月学科教学质量调研数学试卷(解析版) 题型:填空题
如图,A、B是第二象限内双曲线y= 上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=6,则k的值为 .
上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=6,则k的值为 .

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省句容市九年级下学期期中考试(即一模)数学试卷(解析版) 题型:解答题
对某校九 年级随机抽取若干名学生进行体能测试,成绩按A、B、C、D四个等级进行了评定.现将抽取学生的成绩评定结果进行分析,并绘制扇形统计图和条形统计图如下:
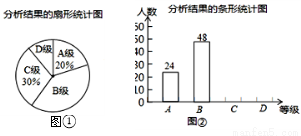
根据上述信息完成下列问题:
(1)这次抽取的样本的容量为 ;图①中“D级”对应的扇形圆心角度数为 °
(2)请在图②中把条形统计图补充完整;
(3)已知该校九年级共有学生750名,请你估计体能达到A级和B级的共约有多少人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com