
【题目】点C是直线l1上一点,在同一平面内,把一个等腰直角三角板ABC任意摆放,其中直角顶点C与点C重合,过点A作直线l2⊥l1,垂足为点M,过点B作l3⊥l1,垂足为点N
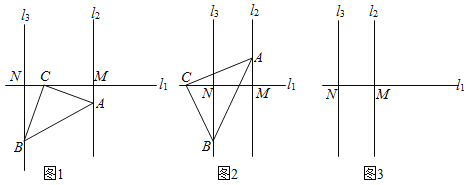
(1)当直线l2,l3位于点C的异侧时,如图1,线段BN,AM与MN之间的数量关系 (不必说明理由);
(2)当直线l2,l3位于点C的右侧时,如图2,判断线段BN,AM与MN之间的数量关系,并说明理由;
(3)当直线l2,l3位于点C的左侧时,如图3,请你补全图形,并直接写出线段BN,AM与MN之间的数量关系.
【答案】(1)MN=AM+BN;(2)MN=BN-AM,见解析;(3)见解析,MN=AM﹣BN.
【解析】
(1)利用AAS定理证明△NBC≌△MCA,根据全等三角形的性质、结合图形解答;
(2)根据直角三角形的性质得到∠CAM=∠BCN,证明△NBC≌△MCA,根据全等三角形的性质、结合图形解答;
(3)根据题意画出图形,仿照(2)的作法证明.
(1)MN=AM+BN
(2)MN=BN-AM
理由如下:如图2.
因为l2⊥l1,l3⊥l1
所以∠BNC=∠CMA=90°
所以∠ACM+∠CAM=90°
因为∠ACB=90°
所以∠ACM+∠BCN=90°
所以∠CAM=∠BCN
又因为CA=CB
所以△CBN≌△ACM(AAS)
所以BN=CM,NC=AM
所以MN=CM﹣CN=BN﹣AM
(3)补全图形,如图3
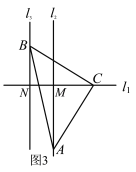
结论:MN=AM﹣BN
由(2)得,△CBN≌△ACM(AAS).
∴BN=CM,NC=AM
结论:MN=CN-CM=AM-BN.


科目:初中数学 来源: 题型:
【题目】如图,某长方形广场的四个角都有一个半径相同的四分之一圆形的草地,若圆形的半径为x米,长方形长为a米,宽为b米
(1)分别用代数式表示草地和空地的面积;
(2)若长方形长为300米,宽为200米,圆形的半径为10米,求广场空地的面积(计算结果保留到整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与直线
与直线![]() 交于A(a,8)B两点,点P是抛物线上A、B之间的一个动点,过点P分别作
交于A(a,8)B两点,点P是抛物线上A、B之间的一个动点,过点P分别作![]() 轴、
轴、![]() 轴的平行线与直线AB交于点C和点E.
轴的平行线与直线AB交于点C和点E.
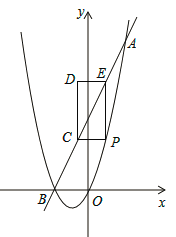
(1)求抛物线的解析式;
(2)若C 为AB中点,求PC的长;
(3)如图,以PC,PE为边构造矩形PCDE,设点D的坐标为(m,n),请求出m,n之间的关系式。
查看答案和解析>>
科目:初中数学 来源: 题型:
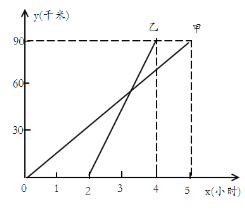
【题目】如图表示甲骑摩托车和乙驾驶汽车沿相同的路线行驶90千米,由A地到B地时,行驶的路程y(千米)与经过的时间x(小时)之间的关系。请根据图象填空:
(1)摩托车的速度为_____千米/小时;汽车的速度为_____千米/小时;
(2)汽车比摩托车早_____小时到达B地。
(3)在汽车出发后几小时,汽车和摩托车相遇?说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AE,∠B=∠E,BC=ED,点F是CD的中点,

(1)AC与AD相等吗?为什么?
(2)AF与CD的位置关系如何?说明理由;
(3)若P为AF上的一点,那么PC与PD相等吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顶点M在y轴上的抛物线与直线y=x+1相交于A、B两点,且点A在x轴上,点B的横坐标为2,连结AM、BM.
(1)求抛物线的函数关系式;
(2)判断△ABM的形状,并说明理由;
(3)把抛物线与直线y=x的交点称为抛物线的不动点.若将(1)中抛物线平移,使其顶点为(m,2m),当m满足什么条件时,平移后的抛物线总有不动点.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的顶点A在△ECD的斜边DE上

(1)求证:AE2+AD2=2AC2;
(2)如图2,若AE=2,AC=2![]() ,点F是AD的中点,直接写出CF的长是 .
,点F是AD的中点,直接写出CF的长是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com