
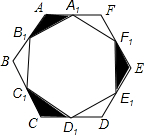
 如图,已知边长为2cm的正六边形ABCDEF,点A1,B1,C1,D1,E1,F1分别为所在各边的中点,则图中阴影部分的总面积是( )
如图,已知边长为2cm的正六边形ABCDEF,点A1,B1,C1,D1,E1,F1分别为所在各边的中点,则图中阴影部分的总面积是( )| A. | $\frac{3\sqrt{3}}{4}$ | B. | $\frac{2\sqrt{3}}{4}$ | C. | $\frac{\sqrt{3}}{4}$ | D. | $\frac{\sqrt{3}}{8}$ |
分析 六边形ABCDEF和A1B1C1D1E1F1都是正多边形,两个多边形的面积的差的一半就是阴影部分的面积.
解答 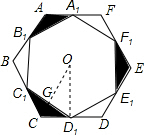 解:边长是2cm的正六边形ABCDEF的面积是:6×$\frac{1}{2}$×sin60°×22=6$\sqrt{3}$cm2.
解:边长是2cm的正六边形ABCDEF的面积是:6×$\frac{1}{2}$×sin60°×22=6$\sqrt{3}$cm2.
作出连接中心O,连接OD1,OC.
在直角△OCD1中,∠O=30°,CD1=$\frac{1}{2}$CD=1(cm).
则OD1=$\sqrt{3}$CD1=$\sqrt{3}$,OG=$\frac{1}{2}$OD1=$\frac{\sqrt{3}}{2}$,C1D1=$\sqrt{3}$.
则A1B1C1D1E1F1的面积是:6×$\frac{1}{2}$×sin60°×($\sqrt{3}$)2=$\frac{9\sqrt{3}}{2}$cm2.
则图中阴影部分的总面积是$\frac{1}{2}$(6$\sqrt{3}$-$\frac{9\sqrt{3}}{2}$)=$\frac{3\sqrt{3}}{4}$.
故选A.
点评 本题考查了正多边形的计算,正多边形的计算常用的方法是转化为正多边形的计算,理解两个多边形的面积的差的一半就是阴影部分的面积是关键.


 星级口算天天练系列答案
星级口算天天练系列答案科目:初中数学 来源: 题型:选择题
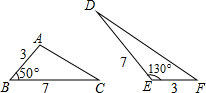 如图,若△ABC和△DEF的面积分别为S1,S2,则( )
如图,若△ABC和△DEF的面积分别为S1,S2,则( )| A. | S1=$\frac{1}{2}$S2 | B. | S1=$\frac{7}{2}$S2 | C. | S1=$\frac{8}{5}$S2 | D. | S1=S2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲比乙稳定 | B. | 乙比甲稳定 | C. | 甲和乙一样稳定 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
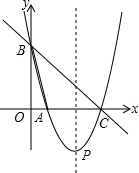 如图,直线y=-x+4与x轴、y轴分别交于点C、B,抛物线y=ax2+bx+c经过点B、C,并与x轴交于另一点A,其顶点为P,tan∠OAB=4.
如图,直线y=-x+4与x轴、y轴分别交于点C、B,抛物线y=ax2+bx+c经过点B、C,并与x轴交于另一点A,其顶点为P,tan∠OAB=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
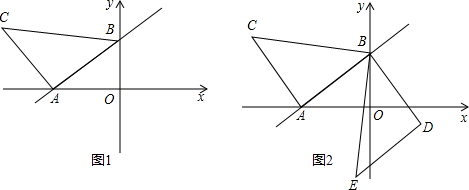
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com