
【题目】如图,点![]() 在矩形
在矩形![]() 的边
的边![]() 上,
上,![]() ,
,![]() ,连接
,连接![]() ,线段
,线段![]() 绕点
绕点![]() 旋转
旋转![]() ,得到线段
,得到线段![]() ,以线段
,以线段![]() 为直径做
为直径做![]() .
.
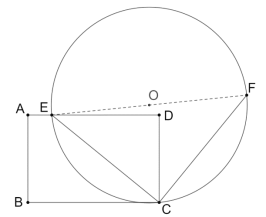

(1)请说明点![]() 一定在
一定在![]() 上的理由,
上的理由,
(2)①点![]() 在
在![]() 上,
上,![]() 为
为![]() 的直径,求证:点
的直径,求证:点![]() 到
到![]() 的距离等于线段
的距离等于线段![]() 的长.
的长.
②当![]() 面积取得最大值时,求
面积取得最大值时,求![]() 半径的长.
半径的长.
(3)当![]() 与矩形
与矩形![]() 的边相切时,计算扇形
的边相切时,计算扇形![]() 的面积.
的面积.
【答案】(1)证明见解析;(2)①证明见解析,②![]() ;(3)
;(3)![]()
【解析】
(1)由CE=CF且∠ECF=90°,O为EF中点,可知OC=OE=OF=![]() ,即E,F,C三点共圆;
,即E,F,C三点共圆;
(2)①作MN⊥AD交AD于点N,连MC,MF,AC,由![]() 为
为![]() 的直径,且四边形ABCD为矩形可证得∠DCE=∠MEN,由CM为直径,可得
的直径,且四边形ABCD为矩形可证得∠DCE=∠MEN,由CM为直径,可得![]() ,由(1)知∠FEC=45°,则可得∠MEO=45°,则易知∠EMO=45°,可得MC⊥EF,可证得四边形ECFN为正方形,所以EC=EM,可证△MEN≌△ECD,即MN=ED,证得M到AD的距离等于ED的长;
,由(1)知∠FEC=45°,则可得∠MEO=45°,则易知∠EMO=45°,可得MC⊥EF,可证得四边形ECFN为正方形,所以EC=EM,可证△MEN≌△ECD,即MN=ED,证得M到AD的距离等于ED的长;
②设AE=x,则![]() ,
,![]() ,
,![]() ,即当x=3时,△AME面积有最大值为
,即当x=3时,△AME面积有最大值为![]() ,由
,由![]() 可知
可知![]() ,即
,即![]() ,而
,而![]() ,由
,由![]() ,求得
,求得![]() ,即
,即![]() 的半径为
的半径为![]() ;
;
(3)![]() 与矩形
与矩形![]() 的边相切时,点O与点D重合,CO=MO为直径,且长为4,则可求得
的边相切时,点O与点D重合,CO=MO为直径,且长为4,则可求得![]() .
.
解:(1)依题意可知,CE=CF且∠ECF=90°,O为EF中点,
∴OC=OE=OF=![]() ,
,
∴点E,F,C三点在![]() 上;
上;
(2)①作MN⊥AD交AD于点N,连MC,MF,AC,
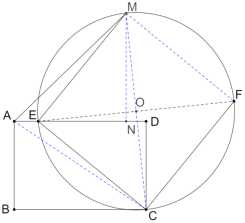
∵![]() 为
为![]() 的直径,
的直径,
∴∠DEC+∠DEM=90°,
∵四边形ABCD为矩形,
∴∠DEC+∠DCE=90°
∴∠DCE=∠MEN,
∵CM为直径,
∴![]() ,
,
由(1)知∠FEC=45°,
∴∠MEO=45°,
∵OM=OE,
∴∠EMO=45°,
∴MC⊥EF,
∴四边形ECFN为正方形,
∴EC=EM,
在△MEN和△ECD中,
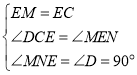 ,
,
所以△MEN≌△ECD,
∴MN=ED,
∴M到AD的距离等于ED的长;
②设AE=x,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴当x=3时,△AME面积有最大值为![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
即![]() 的半径为
的半径为![]() ;
;
(3)![]() 与矩形
与矩形![]() 的边相切时,点O与点D重合CO,MO为直径,长为4,
的边相切时,点O与点D重合CO,MO为直径,长为4,
∴![]() .
.


科目:初中数学 来源: 题型:
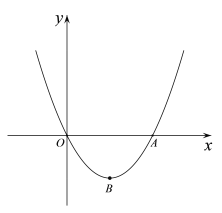
【题目】如图,抛物线y=x2+mx(m<0)交x轴于O,A两点,顶点为点B.
(1)求△AOB的面积(用含m的代数式表示);
(2)直线y=kx+b(k>0)过点B,且与抛物线交于另一点D(点D与点A不重合),交y轴于点C.过点C作CE∥AB交x轴于点E.
(ⅰ) 若∠OBA=90°,2<![]() <3,求k的取值范围;
<3,求k的取值范围;
(ⅱ) 求证:DE∥y轴.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠A=90°.
(1)请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切(保留作图痕迹,不写作法和证明);

(2)在(1)的条件下,若∠B=45°,AB=1,⊙P切BC于点D,求劣弧![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠ADE、∠CDF分别交BC、AB于点E、F,DF交对角线AC于点M,且∠ADE=∠CDF.
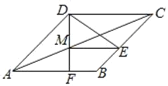
(1)求证:CE=AF;
(2)连接ME,若![]() =
=![]() ,AF=2,求
,AF=2,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中放入![]() 个大小形状几乎完全相同实验用的鸡蛋,鸡蛋的质量有微小的差距(用手感觉不到差异),质量分别为
个大小形状几乎完全相同实验用的鸡蛋,鸡蛋的质量有微小的差距(用手感觉不到差异),质量分别为![]() 、
、![]() 、
、![]() 克,已知随机的摸出一个鸡蛋,摸到
克,已知随机的摸出一个鸡蛋,摸到![]() 克和
克和![]() 克的鸡蛋的概率是相等的.
克的鸡蛋的概率是相等的.
(1)求这四个鸡蛋质量的众数和中位数
(2)小明做实验需要拿走一个鸡蛋,芳芳在小明拿走后从剩下的三个鸡蛋中随机的拿走一个
①通过计算分析小明拿走一个鸡蛋后,剩下的三个鸡蛋质量的中位数是多少?
②假设小明拿走的鸡蛋质量为![]() 克,芳芳随机的拿出一个鸡蛋后又放回,之后再随机的拿出一个鸡蛋,请用树状图求芳芳两次拿到都是
克,芳芳随机的拿出一个鸡蛋后又放回,之后再随机的拿出一个鸡蛋,请用树状图求芳芳两次拿到都是![]() 克的鸡蛋的概率?
克的鸡蛋的概率?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,AC为直径,点D为弧ACB的中点,过点D的切线与BC的延长线交于点E.
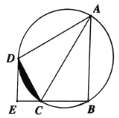
(1)用尺规作图作出圆心O;(保留作图痕迹,不写作法);
(2)求证:DE⊥BC;
(3)若OC=2CE=4,求图中阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与反比例函数
,与反比例函数![]() 的图象的一个交点为
的图象的一个交点为![]() .
.
(1)直接写出反比例函数的解析式;
(2)过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,设点
,设点![]() 在反比例函数图象上,且△PBC的面积等于
在反比例函数图象上,且△PBC的面积等于![]() ,请求出点
,请求出点![]() 的坐标;
的坐标;
(3)设M是直线AB上一动点,过点M作MN//x轴,交反比例函数![]() 的图象于点N,若以B、O、M、N为顶点的四边形为平行四边形,请直接写出点M的坐标.
的图象于点N,若以B、O、M、N为顶点的四边形为平行四边形,请直接写出点M的坐标.
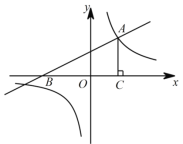
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=8°,点P在OB上.以点P为圆心,OP为半径画弧,交OA于点P1(点P1与点O不重合),连接PP1;再以点P1为圆心,OP为半径画弧,交OB于点P2(点P2与点P不重合),连接P1P2;再以点P2为圆心,OP为半径画弧,交OA于点P3(点P3与点P1不重合),连接P2P3;…按照这样的方法一直画下去,得到点Pn,若之后就不能再画出符合要求的点Pn+1,则n等于( )
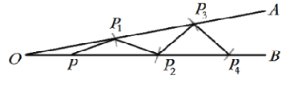
A.13B.12C.11D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情期间,部分小区出现防疫物资紧缺,某爱心组织紧急筹集了部分资金,计划购买甲、乙两种防疫物品共2000件送往各小区,已知每件甲种物品的价格比每件乙种物品的价格贵10元,用350元购买甲种物品的件数恰好与用300元购买乙种物品的件数相同
(1)求甲、乙两种防疫物品每件的价格各是多少元?
(2)经调查,各小区对乙种物品件数的需求量是甲种物品件数的3倍,若该爱心组织按照此需求的比例购买这2000件物品,需筹集资金多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com