
【题目】如图,在菱形ABCD中,∠ADE、∠CDF分别交BC、AB于点E、F,DF交对角线AC于点M,且∠ADE=∠CDF.
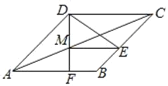
(1)求证:CE=AF;
(2)连接ME,若![]() =
=![]() ,AF=2,求
,AF=2,求![]() 的长.
的长.
【答案】(1)见解析(2)2
【解析】
(1)通过已知条件,易证△ADF≌△CDE,即可求得;
(2)根据![]() =
=![]() ,易求得BE和BF,根据已知条件可得
,易求得BE和BF,根据已知条件可得![]() =
=![]() =
=![]() ,证明△AMF∽△CMD,
,证明△AMF∽△CMD,![]() ,再证明△ABC~△MEC,即可求出ME.
,再证明△ABC~△MEC,即可求出ME.
解:(1)∵四边形ABCD是菱形,
∴AD=CD,∠DAF=∠DCE,
又∵∠ADE=∠CDF,
∴∠ADE﹣∠EDF=∠CDF﹣∠EDF,
∴∠ADF=∠CDE,
在△ADF和△CDE中,
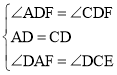 ,
,
∴△ADF≌△CDE,
∴CE=AF.
(2)∵四边形ABCD是菱形,
∴AB=BC,
由(1)得:CE=AF=2,
∴BE=BF,
设BE=BF=x,
∵![]() =
=![]() ,AF=2,
,AF=2,
∴![]() ,解得x=
,解得x=![]() ,
,
∴BE=BF=![]() ,
,
∵![]() =
=![]() ,且CE=AF,
,且CE=AF,
∴![]() =
=![]() =
=![]() ,
,
∵∠CMD=∠AMF,∠DCM=∠AMF,
∴△AMF∽△CMD,
∴![]() ,
,
∴![]() ,且∠ACB=∠ACB,
,且∠ACB=∠ACB,
∴△ABC~△MEC,
∴∠CAB=∠CME=∠ACB,
∴ME=CE=2.


科目:初中数学 来源: 题型:
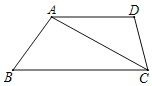
【题目】如图,在四边形ABCD中,AD∥BC.
(1)求作直线EF使得EF交AD于点E,交BC于点F且使得EA=EC,FA=FC(尺规作图,保留作图痕迹,不写作法);
(2)连接AF、CE,判断四边形AFCE的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
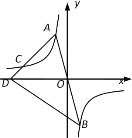
【题目】如图,点A,B,C在反比例函数![]() 的图象上,且直线AB经过原点,点C在第二象限上,连接AC并延长交x轴于点D,连接BD,若△BOD的面积为9,则
的图象上,且直线AB经过原点,点C在第二象限上,连接AC并延长交x轴于点D,连接BD,若△BOD的面积为9,则![]() =_____.
=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
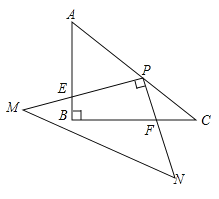
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,Rt△MPN,∠MPN=90°,点P在AC上,PM交AB与点E,PN交BC与点F,当PE=2PF时,AP=_____
查看答案和解析>>
科目:初中数学 来源: 题型:
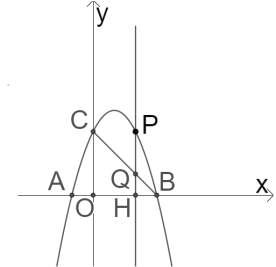
【题目】如图,抛物线y=-x2+bx+c与x轴交于A(-1,0),B两点,与y轴交于点C(0,3),点P是抛物线在第一象限上的一点,过点P作PH⊥x轴,垂足为H,交线段BC于点Q.
(1)求抛物线对应的函数表达式;
(2)当PQ=2QH时,求点P的坐标;
(3)当PH最大时,连接AP,AP与BC交于点D,点F是第一象限内一点,且∠AFC=45°,点G在抛物线上,直线FG、FC分别与直线PH交于点M、N.当三角形ABD相似三角形FMN时,求点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一边长为![]() 的等边
的等边![]() 游乐场,某人从边
游乐场,某人从边![]() 中点
中点![]() 出发,先由点
出发,先由点![]() 沿平行于
沿平行于![]() 的方向运动到
的方向运动到![]() 边上的点
边上的点![]() ,再由
,再由![]() 沿平行于
沿平行于![]() 方向运动到
方向运动到![]() 边上的点
边上的点![]() ,又由点
,又由点![]() 沿平行于
沿平行于![]() 方向运动到
方向运动到![]() 边上的点
边上的点![]() ,则此人至少要运动_______
,则此人至少要运动_______![]() ,才能回到点
,才能回到点![]() .如果此人从
.如果此人从![]() 边上意一点出发,按照上面的规律运动,则此人至少走______
边上意一点出发,按照上面的规律运动,则此人至少走______![]() ,就能回到起点.
,就能回到起点.
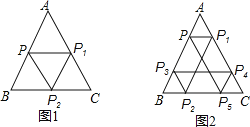
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 在矩形
在矩形![]() 的边
的边![]() 上,
上,![]() ,
,![]() ,连接
,连接![]() ,线段
,线段![]() 绕点
绕点![]() 旋转
旋转![]() ,得到线段
,得到线段![]() ,以线段
,以线段![]() 为直径做
为直径做![]() .
.
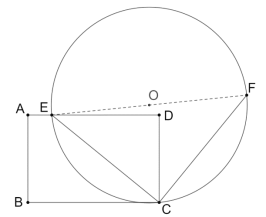

(1)请说明点![]() 一定在
一定在![]() 上的理由,
上的理由,
(2)①点![]() 在
在![]() 上,
上,![]() 为
为![]() 的直径,求证:点
的直径,求证:点![]() 到
到![]() 的距离等于线段
的距离等于线段![]() 的长.
的长.
②当![]() 面积取得最大值时,求
面积取得最大值时,求![]() 半径的长.
半径的长.
(3)当![]() 与矩形
与矩形![]() 的边相切时,计算扇形
的边相切时,计算扇形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
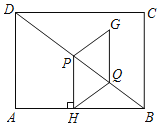
【题目】如图,在矩形ABCD中,AB=4,BC=3,点P,Q在对角线BD上,且BQ=![]() BP,过点P作PH⊥AB于点H,连接HQ,以PH、HQ为邻边作平行四边形PHQG,设BQ=m.
BP,过点P作PH⊥AB于点H,连接HQ,以PH、HQ为邻边作平行四边形PHQG,设BQ=m.
(1)若m=2时,求此时PH的长.
(2)若点C,G,H在同一直线上时,求此时的m值.
(3)若经过点G的直线将矩形ABCD的面积平分,同时该直线将平行四边形PHQG的面积分成1:3的两部分,求此时m的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com