
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() 是腰
是腰![]() 上一个动点(不含点
上一个动点(不含点![]() ),作
),作![]() 交
交![]() 于点
于点![]() (如图1)
(如图1)
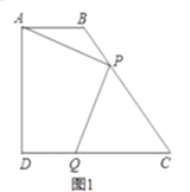
求:(1)BC的长和梯形![]() 的面积;
的面积;
(2)当![]() 时,求
时,求![]() 的长;(如图2)
的长;(如图2)
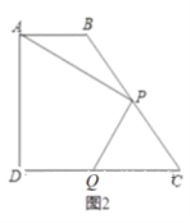
(3)设![]() 试求出
试求出![]() 关于
关于![]() 的函数解析式,并写出定义域
的函数解析式,并写出定义域
【答案】(1)![]() ,
,![]() ;;(2)
;;(2)![]() ;(3)
;(3)![]() ,
,
定义域为(![]() )
)
【解析】
(1)过B作BH⊥CD于H,在Rt△BHC中,根据BH(即AD)的长及∠C的正切值,可求得CH的长,进而可根据勾股定理求得BC的长;得到CH的长,由CD=DH+CH=AB+CH即可得到CD的长,根据梯形的面积公式可求出梯形ABCD的面积;
(2)当PQ=DQ时,连接AQ,易证得△ADQ≌△APQ,则AD=AP=4;过P作PE⊥AB于E,不难得出∠C=∠PBE;可根据∠PBE的正切值,用未知数表示出BE、PE的长,进而在Rt△APE中,由勾股定理求得未知数的值,进而可在Rt△BPE中求出BP的长;
(3)过P作PF⊥CD于F,由于∠APQ=90°,易证得△AEP∽△PFQ,根据得到的比例线段即可用![]() 表示出QF的长,进而可在Rt△PFC中,根据∠C的正切值用
表示出QF的长,进而可在Rt△PFC中,根据∠C的正切值用![]() 表示出CF的长;由CQ=QF+CF即可得到
表示出CF的长;由CQ=QF+CF即可得到![]() 的函数关系式.
的函数关系式.
(1)作BH⊥CD,垂足为H,
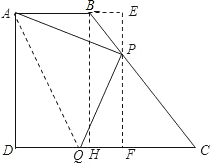
则四边形ABHD为矩形;
∴BH=DA=4,DH=AB=2;
在Rt△BCH中,![]() ,
,
∴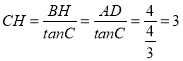 ,
,
∴![]() ;
;
又CD=CH+DH=5,
∴![]() ;
;
(2)连接AQ,
由DQ=PQ,可知△ADQ≌△APQ,AP=AD=4;
作PE⊥AB交AB的延长线于点E,
在Rt△BPE中,![]() ,
,
令BE=3k,PE=4k,
则在Rt△APE中,AP2=AE2+PE2,
即![]() ,解得:
,解得:![]() ,
,
∴![]() ;
;
(3)作PF⊥CD交CD于点F,
∵![]() ,
,
由(2)得:![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由∠AEF=∠EFD=∠APQ=90°,
∴∠APE+∠PAE=90°,∠APE +∠QPF=90°,
∴∠PAE=∠QPF,
∴△AEP∽△PFQ;
∴![]() ,即
,即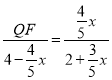 ,
,
化简得:![]() ,
,
又![]() ,
,
∴![]() ;
;
定义域为(![]() ) .
) .


 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() (
(![]() )经过点
)经过点![]() 、B.
、B.
(1)求![]() 、
、![]() 满足的关系式及
满足的关系式及![]() 的值.
的值.
(2)当![]() 时,若
时,若![]() (
(![]() )的函数值随
)的函数值随![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】诗词是我国古代文化中的瑰宝,某市教育主管部门为了解本市初中生对诗词的学习情况,举办了一次“中华诗词”背诵大赛,随机抽取了部分同学的成绩(x为整数,总分100分),绘制了如下尚不完整的统计图表.
组别 | 成绩分组(单位:分) | 频数 |
A | 50≤x<60 | 40 |
B | 60≤x<70 | a |
C | 70≤x<80 | 90 |
D | 80≤x<90 | b |
E | 90≤x<100 | 100 |
合计 | c |
根据以上信息解答下列问题:
(1)统计表中a= ,b= ,c= ;
(2)扇形统计图中,m的值为 ,“E”所对应的圆心角的度数是 (度);
(3)若参加本次大赛的同学共有4000人,请你估计成绩在80分及以上的学生大约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合.
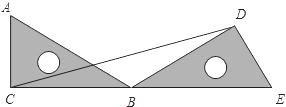
(1)三角尺旋转了 度。
(2)连接CD,试判断△CBD的形状;
(3)求∠BDC的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,DE平分∠ADB,交AB于E,BF平分∠CBD,交CD于F.
(1)求证:△ADE≌△CBF;
(2)当AD与BD满足什么关系时,四边形DEBF是矩形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2+bx+c与x轴交于A(1,0),B(m,0),与y轴交于C.
(1)若m=-3,求抛物线的解析式,并写出抛物线的对称轴;
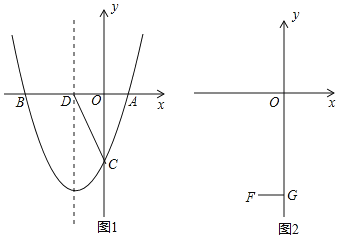
(2)如图1,在(1)的条件下,设抛物线的对称轴交x轴于D,在抛物线对称轴左侧上有 一点E,使S△ACE=S△ACD,求E点的坐标;
(3) 如图2,设F(-1,-4),FG⊥y轴于G,在线段OG上是否存在点P,使 ∠OBP=∠FPG? 若存在,求m的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点坐标分别为A(0,1)、B(3,3)、C(1,3).
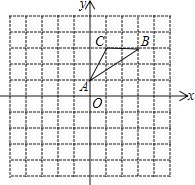
(1) 画出△ABC关于点O的中心对称图形△A1B1C1
(2) 画出△ABC绕原点O逆时针旋转90°的△A2B2C2,直接写出点C2的坐标为______.
(3) 若△ABC内一点P(m,n)绕原点O逆时针旋转90°的对应点为Q,则Q的坐标为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com