
【题目】在![]() 中,
中,![]() ,将
,将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,射线
,射线![]() 与射线
与射线![]() 相交于点
相交于点![]() ,若
,若![]() 是等腰三角形,则
是等腰三角形,则![]() 的度数为__________.
的度数为__________.
【答案】![]() 或36°或
或36°或![]()
【解析】
分三种情形:①当B′E=B′A时,如图1所示.②当EB′=AE时,如图2所示.③如图3中,当B′A=B′E时,分别构建方程求解即可.
解:①当B′E=B′A时,如图1所示:
∵AB=AC,
∴∠B=∠BCA,
由折叠得:∠B=∠B′,∠BCA=∠B′CA,
设∠B=x,则∠B′=∠BCA=∠B′CA=x,
∴∠B′AE=∠B′EA=3x,
在△AEB′中,由内角和定理得:
3x+3x+x=180°,
∴x=![]() ,即:∠B=
,即:∠B=![]() .
.
②当EB′=AE时,如图2所示: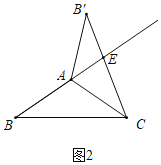
∵AB=AC,
∴∠B=∠BCA,
由折叠得:∠B=∠B′,∠BCA=∠B′CA,
设∠B=x,则∠B′=∠BCA=∠B′CA=x,∠AEB′=3x,
在△AEB′中,由内角和定理得:x+x+3x=180°,
∴x=36°,即∠B=36°.
③如图3中,当B′A=B′E时,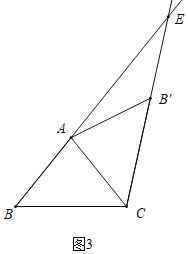
∵AB=AC,
∴∠B=∠BCA,
由折叠得:∠B=∠AB′C,∠BCA=∠B′CA,
设∠B=x,则∠B′=∠BCA=∠B′CA=x,∠AEB′=![]() x,∠EAC=2x,
x,∠EAC=2x,
在△AEC中,由内角和定理得:x+2x+![]() x=180°,
x=180°,
∴x=![]() ,即∠B=
,即∠B=![]() .
.
综上所述,满足条件的∠B的度数为![]() 或36°或
或36°或![]() .
.
故答案为![]() 或36°或
或36°或![]() .
.


科目:初中数学 来源: 题型:
【题目】安九高铁潜山段有甲、乙两个施工队,现中标承建安九高铁一段建设工程.若让两队合作,![]() 天可以完工,需要费用
天可以完工,需要费用![]() 万元;若让两队合作
万元;若让两队合作![]() 天后,剩下的工程由甲队做,还需
天后,剩下的工程由甲队做,还需![]() 天才能完成,这样只需要费用
天才能完成,这样只需要费用![]() 万元.
万元.
(1)甲、乙两队单独完成此项工程各需多少天?
(2)甲、乙两队单独完成此项工程各需费用多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=-x+4的图象与反比例y=![]() (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点.

(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求PA+PB的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 为两条相互平行的直线
为两条相互平行的直线![]() ,
,![]() 之间一点,
之间一点,![]() 和
和![]() 的角平分线相交于
的角平分线相交于![]() ,
,![]() .
.
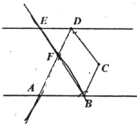

(1)求证:![]() ;
;
(2)连结![]() 当
当![]() 且
且![]() 时,求
时,求![]() 的度数;
的度数;
(3)若![]() 时,将线段
时,将线段![]() 沿直线
沿直线 ![]() 方向平移,记平移后的线段为
方向平移,记平移后的线段为![]() (
(![]() ,
,![]() 分别对应
分别对应![]() 、
、![]() 当
当![]() 时,请直接写出
时,请直接写出![]() 的度数_______.
的度数_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某矩形的面积为20cm 2.
(1)写出其长 y与宽 x之间的函数表达式.
(2)当矩形的长为12cm时,求宽为多少?当矩形的宽为4cm,求其长为多少?
(3)如果要求矩形的长不小于8cm,其宽至多要多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=6,AD=8,矩形内一动点P使得S△PAD=![]() S矩形ABCD,则点P到点A、D的距离之和PA+PD的最小值为_____.
S矩形ABCD,则点P到点A、D的距离之和PA+PD的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要做两个形状相同的三角形框架,其中一个三角形框架的三边的长分别为4、5、6,另一个三角形框架的一边长为2,怎样选料可使这两个三角形相似?你选的木料唯一吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E是AB上一点,DE、CE分别是∠ADC、∠BCD的平分线,若AD=5,DE=6,则平行四边形的面积为( )

A.96B.48C.60D.30
查看答案和解析>>
科目:初中数学 来源: 题型:
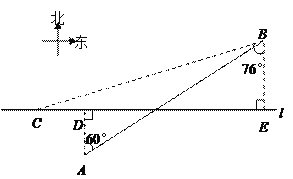
【题目】如图,在航线![]() 的两侧分别有观测点A和B,点A到航线
的两侧分别有观测点A和B,点A到航线![]() 的距离为2km,点B位于点A北偏东60°方向且与A相距10km处.现有一艘轮船从位于点B南偏西76°方向的C处,正沿该航线自西向东航行,5min后该轮船行至点A的正北方向的D处.
的距离为2km,点B位于点A北偏东60°方向且与A相距10km处.现有一艘轮船从位于点B南偏西76°方向的C处,正沿该航线自西向东航行,5min后该轮船行至点A的正北方向的D处.
(1)求观测点B到航线![]() 的距离;
的距离;
(2)求该轮船航行的速度(结果精确到0.1km/h).(参考数据: ![]() 1.73,sin76°≈0.97,cos≈0.24,tan76°≈0.4.01)
1.73,sin76°≈0.97,cos≈0.24,tan76°≈0.4.01)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com