
【题目】安九高铁潜山段有甲、乙两个施工队,现中标承建安九高铁一段建设工程.若让两队合作,![]() 天可以完工,需要费用
天可以完工,需要费用![]() 万元;若让两队合作
万元;若让两队合作![]() 天后,剩下的工程由甲队做,还需
天后,剩下的工程由甲队做,还需![]() 天才能完成,这样只需要费用
天才能完成,这样只需要费用![]() 万元.
万元.
(1)甲、乙两队单独完成此项工程各需多少天?
(2)甲、乙两队单独完成此项工程各需费用多少万元?
【答案】(1)甲,乙两队单独完成该项工作分别需60,90天;(2)甲、乙两队单独完成此项工程各需费用60万元,360万元.
【解析】
(1)设甲,乙两队单独完成该项工作分别需![]() ,
,![]() 天,根据“若让两队合作,
天,根据“若让两队合作,![]() 天可以完工;若让两队合作
天可以完工;若让两队合作![]() 天后,剩下的工程由甲队做,还需
天后,剩下的工程由甲队做,还需![]() 天才能完成”列出方程组,求解即可;
天才能完成”列出方程组,求解即可;
(2)设甲每天需要费用![]() 万元,乙每天需要费用
万元,乙每天需要费用![]() 万元,根据题意列出方程组,分别求出甲,乙每天需要的费用,结合(1)中结果解答即可.
万元,根据题意列出方程组,分别求出甲,乙每天需要的费用,结合(1)中结果解答即可.
解:(1)设甲,乙两队单独完成该项工作分别需![]() ,
,![]() 天.
天.
由题意得: ,
,
解这个方程组得![]() ,
,
经检验得![]() 是原方程的解
是原方程的解
答:甲,乙两队单独完成该项工程分别需60天,90天;
(2)设甲每天需要费用![]() 万元,乙每天需要费用
万元,乙每天需要费用![]() 万元,
万元,
由题意得:
解得![]()
∴甲单独完成此项工程需费用1×60=60(万元),
乙单独完成此项工程需费用4×90=360(万元),
答:甲、乙两队单独完成此项工程各需费用60万元,360万元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
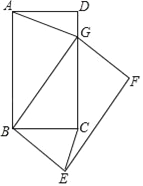
【题目】如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B旋转得到矩形GBEF.
(1)观察发现:在旋转的过程中, ![]() 的值不变,这个数值是 ;
的值不变,这个数值是 ;
(2)问题解决:当点G落在直线CD上时,求CE的长;
(3)数学思考:在旋转的过程中,CE是否有最大值,如果有,请直接写出;如果没有,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:将边长为![]() 的正三角形的三条边分别
的正三角形的三条边分别![]() 等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
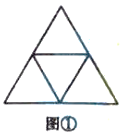
探究:要研究上面的问题,我们不妨先从最简单的情形入手,进而找到一般性规律.
探究一:将边长为2的正三角形的三条边分别二等分,连接各边中点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
如图①,连接边长为2的正三角形三条边的中点,从上往下看:
边长为1的正三角形,第一层有1个,第二层有3个,共有![]() 个;
个;
边长为2的正三角形一共有1个.
探究二:将边长为3的正三角形的三条边分别三等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
如图②,连接边长为3的正三角形三条边的对应三等分点,从上往下看:边长为1的正三角形,第一层有1个,第二层有3个,第三层有5个,共有![]() 个;边长为2的正三角形共有
个;边长为2的正三角形共有![]() 个.
个.

探究三:将边长为4的正三角形的三条边分别四等分(图③),连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
(仿照上述方法,写出探究过程)

结论:将边长为![]() 的正三角形的三条边分别
的正三角形的三条边分别![]() 等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
等分,连接各边对应的等分点,则该三角形中边长为1的正三角形和边长为2的正三角形分别有多少个?
(仿照上述方法,写出探究过程)
应用:将一个边长为25的正三角形的三条边分别25等分,连接各边对应的等分点,则该三角形中边长为1的正三角形有______个和边长为2的正三角形有______个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《代数学》中记载,形如x2+8x=33的方程,求正数解的几何方法是:“如图1,先构造一个面积为x2的正方形,再以正方形的边长为一边向外构造四个面积为2x的矩形,得到大正方形的面积为33+16=49,则该方程的正数解为7﹣4=3.”小聪按此方法解关于x的方程x2+10x+m=0时,构造出如图2所示的图形,已知阴影部分的面积为50,则该方程的正数解为( )


A.6B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】开学初,李芳和王平去文具店购买学习用品,李芳用18元钱买了1支钢笔和3本笔记本;王平用30元买了同样的钢笔2支和笔记本4本.
(1)求每支钢笔和每本笔记本的价格;
(2)校运会后,班主任拿出200元学校奖励基金交给班长,购买上述价格的钢笔笔记本共36件作为奖品,奖给校运会中表现突出的同学,要求笔记本数不多于钢笔数的2倍,共有多少种购买方案?请你一一写出.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于第一、三象限内的
的图象相交于第一、三象限内的![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.

(1)求该反比例函数和一次函数的解析式;
(2)直接写出当![]() 时,
时,![]() 的取值范围;
的取值范围;
(3)在![]() 轴上找一点
轴上找一点![]() 使
使![]() 最大,求
最大,求![]() 的最大值及点
的最大值及点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的方格中,每个小正方形的边长都为1,△ABC的顶点均在格点上.在建立平面直角坐标系后,点B的坐标为(﹣1,2).
(1)把△ABC向下平移8个单位后得到对应的△A1B1C1,画出△A1B1C1,并写出A1坐标是 .
(2)以原点O为对称中心,画出与△ABC关于原点O对称的△A2B2C2,并写出B2坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角△ABC中,D,E分别为AB,BC中点,F为AC上一点,且∠AFE=∠A,DM∥EF交AC于点M.

(1)点G在BE上,且∠BDG=∠C,求证:DGCF=DMEG;
(2)在图中,取CE上一点H,使∠CFH=∠B,若BG=1,求EH的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com