练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．当m=1时，方程（m+1）x${\;}^{{m}^{2}+1}$+（m-3）x-1=0是一元二次方程．

    分析 根据一元二次方程的定义得到m2+1=2且m+1≠0．

    解答 解：依题意得：m2+1=2且m+1≠0．
    解得m=1．
    故答案是：1．

    点评 本题利用了一元二次方程的概念．只有一个未知数且未知数最高次数为2的整式方程叫做一元二次方程，一般形式是ax2+bx+c=0（且a≠0）．特别要注意a≠0的条件．这是在做题过程中容易忽视的知识点．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

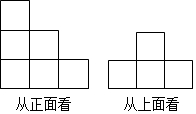    7．用小立方块搭成的几何体，从正面看和从上面看得到的视图如图，问这样的几何体有多少可能？它最多需要多少小立方块，最少需要多少小立方块，请画出最少和最多时从左面看到的视图．
    答：共有2种可能；最多有8 块小立方体； 最少7块小立方体．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．已知抛物线y=x2-2x-3与x轴相交于A、B两点，其顶点为M，将此抛物线在x轴下方的部分沿x轴翻折，其余部分保持不变，得到一个新的图象．如图，当直线y=-x+n与此图象有且只有两个公共点时，则n的取值范围为n＞$\frac{21}{4}$或-1＜n＜3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

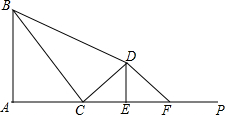    5．如图，∠A=90°，AB=6，点C是射线AP上的动点，连结BC，过点C作CD⊥BC，垂足为C，且BC=2CD，过点D作DE⊥AP于点E，点F是点C关于直线DE的对称点，连接BD、DF，设AC=m．
    （1）当m=2时，求DE的长；
    （2）当m为何值时，点D落在线段BF上；
    （3）过点B作AP的平行线交直线DE于点H，设△BDH的面积为S，用含m的代数式表示S．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知关于x的一元二次方程（a-1）x2-5x+4a-2=0的一个根为x=3．
    （1）求a的值及方程的另一个根；
    （2）如果一个等腰三角形（底和腰不相等）的三边长都是这个方程的根，求这个三角形的周长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．先化简，再求值：$\frac{{m}^{2}-6m+9}{m-3}$-$\frac{\sqrt{{m}^{2}-8m+16}}{{m}^{2}-4m}$-$\frac{1}{m}$，其中m=4-$\sqrt{5}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．已知△ABC≌△A′B′C′，A与A′，B与B′是对应点，△A′B′C′周长为18cm，AB=3cm，BC=4cm，则A′C′=11cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．若a是方程x2-5x-4=0的根，则a2-5a的值为4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．暑假期间，某甜品店为了回馈顾客和促销，准备推出掷骰子（投掷各方面数字为1到6的均匀正方体看面朝上的点数）赢积分劵的活动，游戏规则如下：顾客每次消费后，可同时投掷两枚骰子一次，两枚骰子点数之和写作a，两枚骰子点数之差的绝对值记作x，若0≤x≤2，则n=x；若3≤x≤5，则n=x-3；顾客获得的奖券金额为an元，用于在以后来店消费中抵用现金．
    （1）用树状图或列表法写出a的所有结果；
    （2）计算顾客获得1元奖券的概率；
    （3）计算顾客获得100元以上（含100元）奖券的概率．

    查看答案和解析>>

    同步练习册答案