
 已知抛物线y=x2-2x-3与x轴相交于A、B两点,其顶点为M,将此抛物线在x轴下方的部分沿x轴翻折,其余部分保持不变,得到一个新的图象.如图,当直线y=-x+n与此图象有且只有两个公共点时,则n的取值范围为n>$\frac{21}{4}$或-1<n<3.
已知抛物线y=x2-2x-3与x轴相交于A、B两点,其顶点为M,将此抛物线在x轴下方的部分沿x轴翻折,其余部分保持不变,得到一个新的图象.如图,当直线y=-x+n与此图象有且只有两个公共点时,则n的取值范围为n>$\frac{21}{4}$或-1<n<3. 分析 (1)根据解析式求与x轴交点A、B的坐标,确定二次函数的顶点M,由翻折性质求新抛物线顶点坐标为(1,4),得出新抛物线的解析式;
(2)求直线y=-x+n过两个边界点时对应的n的值,并求直线与新抛物线相切时的n值,继而得出n的取值范围.
解答 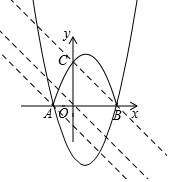 解:当y=0时,y=x2-2x-3=0,
解:当y=0时,y=x2-2x-3=0,
(x-3)(x+1)=0,
x=-1或3,
∴A(-1,0),B(3,0),
y=x2-2x-3=(x-1)2-4,
∴M(1,-4),
如图,作直线y=-x,
分别过A、B作直线y=-x的平行线,
当直线y=-x+n经过A(-1,0)时,1+n=0,n=-1,
当直线y=-x+n经过B(3,0)时,-3+n=0,n=3,
∴n的取值范围为:-1<n<3,
根据题意得:翻折后的顶点坐标为(1,4),
∴翻折后的抛物线的解析式为:y=-(x-1)2+4=-x2+2x+3,
当直线y=-x+n与抛物线y=-x2+2x+3只有一个公共点时,
则$\left\{\begin{array}{l}{y=-x+n}\\{y=-{x}^{2}+2x+3}\end{array}\right.$,
-x2+2x+3=-x+n,
-x2+3x+3-n=0,
△=9+4(3-n)=0,
n=$\frac{21}{4}$,
综上所述:当直线y=-x+n与此图象有且只有两个公共点时,则n的取值范围为n>$\frac{21}{4}$或-1<n<3.
点评 本题考查了抛物线与x轴的交点和几何变换问题,明确抛物线在x轴下方的部分沿x轴翻折,即翻折前后的点关于x轴对称,先求特殊点,即顶点坐标,从而求出翻折后的抛物线的解析式,对于第二问中,同样先求直线过边界时对应的n的值,利用数形结合的思想确定其结果.


科目:初中数学 来源: 题型:选择题
| A. | 没有最大的正数,却有最大的负数 | B. | 数轴上离原点越远,表示数越大 | ||
| C. | 0大于一切负数 | D. | 在原点左边离原点越远,数就越大 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
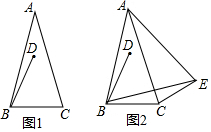 在△ABC中,AB=AC,∠BAC=α(0°<α<60°),BD=BC,∠DBC=60°.
在△ABC中,AB=AC,∠BAC=α(0°<α<60°),BD=BC,∠DBC=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC向外侧作等腰Rt△ABD与Rt△ACE,∠BAD=∠CAE=90°,F为BC的中点,连接F、A并延长交DE于G点,请问:AF与DE之间存在怎样的数量关系和位置关系?
如图,△ABC向外侧作等腰Rt△ABD与Rt△ACE,∠BAD=∠CAE=90°,F为BC的中点,连接F、A并延长交DE于G点,请问:AF与DE之间存在怎样的数量关系和位置关系?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com