
分析 (1)原式利用乘法法则计算即可得到结果;
(2)原式利用除法法则计算即可得到结果;
(3)原式利用减法法则变形,计算即可得到结果;
(4)原式从左到右依次计算即可得到结果;
(5)原式逆用乘法分配律计算即可得到结果;
(6)原式变形后,利用乘法分配律计算即可得到结果;
(7)原式先计算乘方运算,再计算乘法运算,最后算加减运算即可得到结果;
(8)原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.
解答 解:(1)原式=$\frac{9}{2}$×$\frac{10}{3}$=15;
(2)原式=$\frac{12}{5}$×(-$\frac{5}{16}$)=-$\frac{3}{4}$;
(3)原式=12+18-7-15=30-22=8;
(4)原式=81×$\frac{4}{9}$×$\frac{4}{9}$×$\frac{1}{16}$=1;
(5)原式=-3$\frac{6}{7}$×(-5-7+12)=0;
(6)原式=(-20+$\frac{1}{9}$)×9=-180+1=-179;
(7)原式=18-4-80=-66;
(8)原式=-9-9+20=2.
点评 此题考查了有理数的混合运算,熟练掌握运算法则是解本题的关键.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:初中数学 来源: 题型:解答题
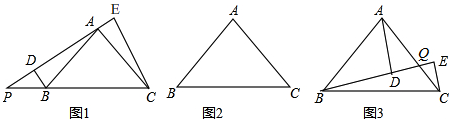
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知抛物线y=x2-2x-3与x轴相交于A、B两点,其顶点为M,将此抛物线在x轴下方的部分沿x轴翻折,其余部分保持不变,得到一个新的图象.如图,当直线y=-x+n与此图象有且只有两个公共点时,则n的取值范围为n>$\frac{21}{4}$或-1<n<3.
已知抛物线y=x2-2x-3与x轴相交于A、B两点,其顶点为M,将此抛物线在x轴下方的部分沿x轴翻折,其余部分保持不变,得到一个新的图象.如图,当直线y=-x+n与此图象有且只有两个公共点时,则n的取值范围为n>$\frac{21}{4}$或-1<n<3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 购买服装的套数 | 1~39套 | 40~79套 | 80套及以上 |
| 每套服装的价格 | 80元 | 70元 | 60元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
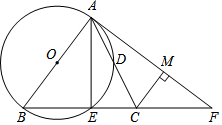 如图,在△ABC中,AB=BC,以AB为直径的⊙O分别交AC,BC于点D,E,过点A作⊙O的切线交BC的延长线于点F,连接AE.
如图,在△ABC中,AB=BC,以AB为直径的⊙O分别交AC,BC于点D,E,过点A作⊙O的切线交BC的延长线于点F,连接AE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com