
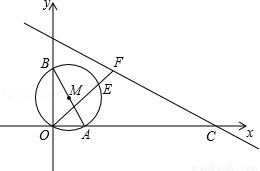
如图,⊙M过坐标原点O,分别交两坐标轴于A(1,O),B(0,2)两点,直线CD交x轴于点C(6,0),交y轴于点D(0,3),过点O作直线OF,分别交⊙M于点E,交直线CD于点F.
(1)求证:∠CDO=∠BAO;
(2)求证:OE•OF=OA•OC;
(3)若OE=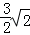 ,试求点F的坐标.
,试求点F的坐标.
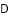
(1)证明见解析
证明见解析
F的坐标为:(2,2)或(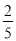 ,
,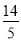 ).
).
【解析】
试题分析:(1)由已知可得tan∠CDO=tan∠BAO所以∠CDO=∠BAO,
(2)连接AE,由圆周角相等则有∠AEO=∠ABO,由(1)则有∠AEO=∠OCD则有△OCF∽△OEA.再利用比例式即可证得.
(3)由(2)可求得OF的长度,因为点F要直线CD上,则可设F(x,y),则可得到关于x,y的方程组,解方程组即可得出点F的坐标
试题解析:(1)如图:∵C(6,0),D(0,3),
∴tan∠CDO=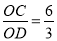 =2,
=2,
∵A(1,O),B(0,2),
cot∠BAO=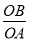 =2,
=2,
∴∠CDO=∠BAO,
(2)如图,连接AE,
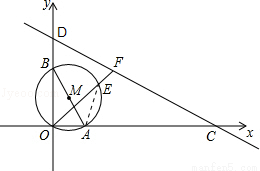
由(1)知∠CDO=∠BAO,
∴∠OCD=∠OBA,
∵∠OBA=∠OEA,
∴∠OCD=∠OEA,
∴△OCF∽△OEA,
∴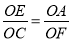
∴OE•OF=OA•OC;
(3)由(2)得OE•OF=OA•OC,
∵OA=1,0C=6,OE=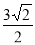 ,
,
∴OF=
设F(x,y)
∴x2+y2=8,
∵直线CD的函数式为:y=﹣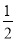 x+3
x+3
∴组成的方程组为 ,
,
解得 或
或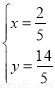
∴F的坐标为:(2,2)或(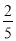 ,
,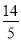 ).
).
考点:1、三角函数;2、圆周角定理;3、相似;4、方程组


科目:初中数学 来源:2014年初中毕业升学考试(福建莆田卷)数学(解析版) 题型:填空题
如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,边AO在y轴上,点B1,B2,B3,…都在直线y= x上,则A2014的坐标是 .
x上,则A2014的坐标是 .

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(福建三明卷)数学(解析版) 题型:选择题
如图,AB是⊙O的直径,弦CD⊥AB于点E,则下列结论正确的是( )

A.DE=BE B.
C.△BOC是等边三角形 D.四边形ODBC是菱形
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(福建三明卷)数学(解析版) 题型:选择题
下列计算正确的是( )
A.(a3)2=a5 B.a6÷a3=a2 C.(ab)2=a2b2 D.(a+b)2=a2+b2
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(甘肃天水卷)数学(解析版) 题型:填空题
如图,一段抛物线y=﹣x(x﹣1)(0≤x≤1)记为m1,它与x轴交点为O、A1,顶点为P1;将m1绕点A1旋转180°得m2,交x轴于点A2,顶点为P2;将m2绕点A2旋转180°得m3,交x轴于点A3,顶点为P3,…,如此进行下去,直至得m10,顶点为P10,则P10的坐标为( ).

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(甘肃兰州卷)数学(解析版) 题型:解答题
如图,在△ABC中,先作∠BAC的角平分线AD交BC于点D,再以AC边上的一点O为圆心,过A、D两点作⊙O(用尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑)
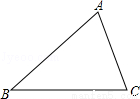
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖南长沙卷)数学(解析版) 题型:选择题
一个关于x的一元一次不等式组的解集在数轴上的表示如图,则该不等式组的解集是( )

A.x>1 B.x≥1 C.x>3 D.x≥3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com