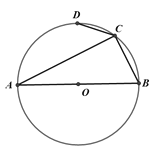
【题目】在⊙O中，AB为直径，∠ACD=45°，已知AC=7，BC=5，则CD =_______
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】齐齐哈尔市教育局想知道某校学生对扎龙自然保护区的了解程度，在该校随机抽取了部分学生进行问卷，问卷有以下四个选项：A．十分了解；B．了解较多：C．了解较少：D．不了解（要求：每名被调查的学生必选且只能选择一项）．现将调查的结果绘制成两幅不完整的统计图．请根据两幅统计图中的信息回答下列问题：
（1）本次被抽取的学生共有_______名；
（2）请补全条形图；
（3）扇形图中的选项“C．了解较少”部分所占扇形的圆心角的大小为_______°；
（4）若该校共有
名学生，请你根据上述调查结果估计该校对于扎龙自然保护区“十分了解”和“了解较多”的学生共有多少名？
查看答案和解析>>
科目：初中数学 来源： 题型：
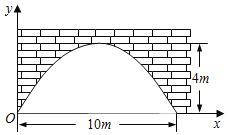
【题目】有一个抛物线形的拱形桥洞，桥洞离水面的最大高度为4m，跨度为10m，如图所示，把它的图形放在直角坐标系中．
(1)求这条抛物线所对应的函数关系式；
(2)一辆宽为2米，高为3米的货船能否从桥下通过？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小东根据学习函数的经验，对函数
的图像与性质进行了探究，下面是小东的探究过程，请补充完整，并解决相关问题：
（1）函数的自变量x的取值范围是__________________
（2）如表示y与x的几组对应值：
x | … |
|
|
|
|
|
|
|
|
|
|
| … |
y | … |
|
|
|
|
|
|
|
|
|
| m | … |
表中m的值为____________
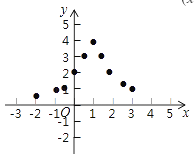
（3）如图，在平面直角坐标系中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出函数的大致图像；
（4）结合函数图像，请写出函数的2条性质：
①__________________________________________________________________________
②__________________________________________________________________________
（5）解决问题：如果函数与直线
的交点有2个，那么a的取值范围是_______________________
（6）
在函数图像上，若
，则m的取值范围______________
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在
中，
，
，
为等边三角形，
，连接
，
为中点．
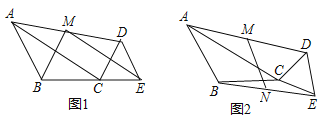
（1）如图1，当
，
，
三点共线时，请画出
关于点的中心对称图形，判断
与
的位置关系是 ；
（2）如图2，当A，，三点共线时，问（1）中结论是否成立，若成立，给出证明，若不成立，请说明理由；
（3）如图2，取
中点
，连
，将绕点旋转，直接写出旋转过程中线段的取值范围是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将一条长为20cm的铁丝剪成两段，并以每一段铁丝的长度为周长做成一个正方形．
(1)要使这两个正方形的面积之和等于17cm2，那么这段铁丝剪成两段后的长度分别是多少?
(2)两个正方形的面积之和可能等于12cm2吗? 若能，求出两段铁丝的长度；若不能，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】中国古代有着辉煌的数学成就，《周牌算经》、《九章算术》、《海岛算经》、《孙子算经》等是我国古代数学的重要文献.
（1）小聪想从这4部数学名著中随机选择1部阅读，求他选中《九章算术》的概率；
（2）小聪拟从这4部数学名著中选择2部作为假课外拓展学习内容，用列表或树状图求选中的名著恰好是《九章算术》和《周牌算经》的概率.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，AB是⊙O的直径，AC是上半圆的弦，过点C作⊙O的切线DE交AB的延长线于点E，过点A作切线DE的垂线，垂足为D，且与⊙O交于点F，设∠DAC，∠CEA的度数分别是α，β．
（1）用含α的代数式表示β，并直接写出α的取值范围；
（2）连接OF与AC交于点O′，当点O′是AC的中点时，求α，β的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
