
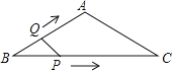
【题目】如图,在等腰△ABC中,AB=AC=4cm,∠B=30°,点P从点B出发,以![]() cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发以2cm/s的速度沿B→A→C运动到点C停止.若△BPQ的面积为y运动时间为x(s),则下列图象中能大致反映y与x之间关系的是( )
cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发以2cm/s的速度沿B→A→C运动到点C停止.若△BPQ的面积为y运动时间为x(s),则下列图象中能大致反映y与x之间关系的是( )
A.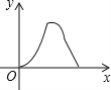 B.
B.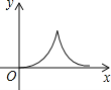 C.
C.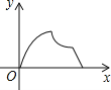 D.
D.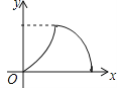
【答案】D
【解析】
作AH⊥BC于H,根据等腰三角形的性质得BH=CH,利用∠B=30°可计算出AH=![]() AB=2,BH=
AB=2,BH=![]() AH=2
AH=2![]() ,BC=2BH=4
,BC=2BH=4![]() ,利用速度公式可得点P从B点运动到C需4s,Q点运动到C需8s,然后分类讨论:当0≤x≤2时,作QD⊥BC于D,如图1;当2<x≤4时,作QD⊥BC于D,如图2;于是可得0≤x≤2时,函数图象为抛物线的一部分,当2<x≤4时,函数图象为抛物线的一部分,即可得到答案.
,利用速度公式可得点P从B点运动到C需4s,Q点运动到C需8s,然后分类讨论:当0≤x≤2时,作QD⊥BC于D,如图1;当2<x≤4时,作QD⊥BC于D,如图2;于是可得0≤x≤2时,函数图象为抛物线的一部分,当2<x≤4时,函数图象为抛物线的一部分,即可得到答案.
解:如图1,作AH⊥BC于H,
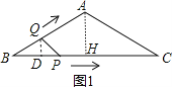
∵AB=AC=4cm,
∴BH=CH
∵∠B=30°,
∴AH=![]() AB=2,BH=
AB=2,BH=![]() AH=2
AH=2![]() ,
,
∴BC=2BH=4![]() ,
,
∵点P运动的速度为![]() cm/s,Q点运动的速度为2cm/s,
cm/s,Q点运动的速度为2cm/s,
∴点P从B点运动到C需2![]() s,Q点运动到C需4s,
s,Q点运动到C需4s,
当0≤x≤2时,作QD⊥BC于D,如图1,BQ=2x,BP=![]() ,
,

在Rt△BPQ中,DQ=![]() BQ=x,
BQ=x,
∴y=![]() x
x![]() x=
x=![]() x2.
x2.
当2<x≤4时,作QD⊥BC于D,如图2,CQ=4-2x,BP=![]() x,
x,
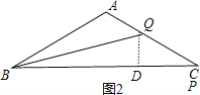
在Rt△BDQ中,DQ=![]() =
=![]() (4-2x),
(4-2x),
∴y=![]() (4-2x)
(4-2x)![]() =
=![]() ,
,
综上所述,y=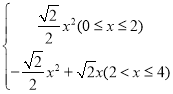
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,直线y=﹣x+5与x轴交于点B,与y轴交于点D,抛物线y=﹣x2+bx+c与直线y=﹣x+5交于B,D两点,点C是抛物线的顶点.

(1)求抛物线的解析式;
(2)点M是直线BD上方抛物线上的一个动点,其横坐标为m,过点M作x轴的垂线,交直线BD于点P,当线段PM的长度最大时,求m的值及PM的最大值;
(3)在抛物线上是否存在异于B、D的点Q,使△BDQ中BD边上的高为3![]() ,若存在求出点Q的坐标;若不存在请说明理由.
,若存在求出点Q的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 今年5月份,我市某中学开展争做“五好小公民”征文比赛活动,赛后随机抽取了部分参赛学生的成绩,按得分划分为A,B,C,D四个等级,并绘制了如下不完整的频数分布表和扇形统计图:
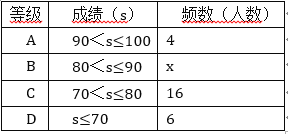
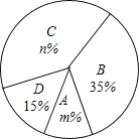
根据以上信息,解答以下问题:
(1)表中的x=______;
(2)扇形统计图中m=______,n=______,C等级对应的扇形的圆心角为______度;
(3)该校准备从上述获得A等级的四名学生中选取两人做为学校“五好小公民”志愿者,已知这四人中有两名男生(用a1,a2表示)和两名女生(用b1,b2表示),请用列表或画树状图的方法求恰好选取的是a1和b1的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为![]() .双曲线
.双曲线![]() 的图象经过BC的中点D,且与AB交于点E,连接DE.
的图象经过BC的中点D,且与AB交于点E,连接DE.
(1)求k的值及点E的坐标;
(2)若点F是OC边上一点,且△FBC∽△DEB,求直线FB的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学活动小组为测量学校旗杆AB的高度,沿旗杆正前方![]() 米处的点C出发,沿斜面坡度
米处的点C出发,沿斜面坡度![]() 的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB//DE.求旗杆AB的高度.(参考数据:sin37°≈
的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A、B、C、D、E在同一平面内,AB⊥BC,AB//DE.求旗杆AB的高度.(参考数据:sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() .计算结果保留根号)
.计算结果保留根号)
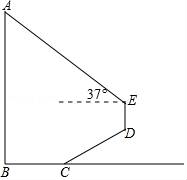
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校积极开展中学生社会实践活动,决定成立文明宣传、环境保护、交通监督三个志愿者队伍,每名学生最多选择一个队伍,为了了解学生的选择意向,随机抽取A,B,C,D四个班,共200名学生进行调查.将调查得到的数据进行整理,绘制成如下统计图(不完整)
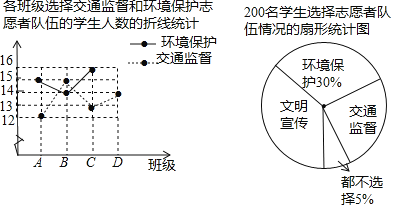
(1)求扇形统计图中交通监督所在扇形的圆心角度数;
(2)求D班选择环境保护的学生人数,并补全折线统计图;(温馨提示:请画在答题卷相对应的图上)
(3)若该校共有学生2500人,试估计该校选择文明宣传的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
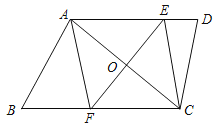
【题目】如图,在四边形ABCD中,AD∥BC,点O是对角线AC的中点,过点O作AC的垂线,分别交AD、BC于点E、F,连结AF、CE.
(1)求证:△AOE≌△COF.
(2)试判断四边形AFCE的形状,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】山西是我国酿酒最早的地区之一,山西酿酒业迄今为止已有![]() 余年的历史.在漫长的历史进程中,山西人民酿造出品种繁多、驰名中外的美酒佳酿,其中以汾酒、竹叶青酒最为有名.某烟酒超市卖有竹叶青酒,每瓶成本价是
余年的历史.在漫长的历史进程中,山西人民酿造出品种繁多、驰名中外的美酒佳酿,其中以汾酒、竹叶青酒最为有名.某烟酒超市卖有竹叶青酒,每瓶成本价是![]() 元,经调查发现,当售价为
元,经调查发现,当售价为![]() 元时,每天可以售出
元时,每天可以售出![]() 瓶,售价每降低
瓶,售价每降低![]() 元,可多售出
元,可多售出![]() 瓶(售价不高于
瓶(售价不高于![]() 元)
元)
(1)售价为多少时可以使每天的利润最大?最大利润是多少?
(2)要使每天的利润不低于![]() 元,每瓶竹叶青酒的售价应该控制在什么范围内?
元,每瓶竹叶青酒的售价应该控制在什么范围内?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读以下材料,并按要求完成相应的任务.
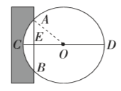
“圆材埋壁”是我国古代数学著作《九章算术》中的一个问题:今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?用现在的数学语言表达是:如图,![]() 为
为![]() 的直径,弦
的直径,弦![]() ,垂足为
,垂足为![]() ,
,![]() 寸,
寸,![]() 尺,其中1尺
尺,其中1尺![]() 寸,求出直径
寸,求出直径![]() 的长.
的长.
解题过程如下:
连接![]() ,设
,设![]() 寸,则
寸,则![]() 寸.
寸.
∵![]() 尺,∴
尺,∴![]() 寸.
寸.
在![]() 中,
中,![]() ,即
,即![]() ,解得
,解得![]() ,
,
∴![]() 寸.
寸.
任务:
(1)上述解题过程运用了 定理和 定理.
(2)若原题改为已知![]() 寸,
寸,![]() 尺,请根据上述解题思路,求直径
尺,请根据上述解题思路,求直径![]() 的长.
的长.
(3)若继续往下锯,当锯到![]() 时,弦
时,弦![]() 所对圆周角的度数为 .
所对圆周角的度数为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com