
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:选择题
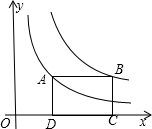 已知:如图,四边形ABCD是矩形,其中点A(x1,a)、B(x2,a)分别是函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$上第一象限的点,点C、D在x轴上.在边AD从大于AB到小于AB的变化过程中,若矩形ABCD的周长始终保持不变,则(k2-k1)的值的变化情况是( )
已知:如图,四边形ABCD是矩形,其中点A(x1,a)、B(x2,a)分别是函数y=$\frac{{k}_{1}}{x}$和y=$\frac{{k}_{2}}{x}$上第一象限的点,点C、D在x轴上.在边AD从大于AB到小于AB的变化过程中,若矩形ABCD的周长始终保持不变,则(k2-k1)的值的变化情况是( )| A. | 一直增大 | B. | 一直减小 | C. | 先增大后减小 | D. | 先减小后增大 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{y}{5x}÷\frac{1}{3}x=\frac{y}{5x}•3x=\frac{3}{5}y$ | |
| B. | $8xy÷\frac{4x}{y}=\frac{1}{8xy}•\frac{4x}{y}=\frac{1}{2{y}^{2}}$ | |
| C. | $\frac{x}{2a}÷\frac{2b}{y}=\frac{x}{2a}•\frac{y}{2b}=\frac{xy}{2ab}$ | |
| D. | $\frac{x+y}{{x}^{2}-xy}÷\frac{1}{x-y}=\frac{x+y}{x(x-y)}•(x-y)=\frac{x+y}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
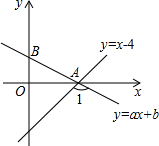 如图,已知直线y=x-4与x轴交于点A,直线y=ax+b也经过点A,且与y轴的正半轴交于点B,若∠1=105°,则直线AB的解析式为( )
如图,已知直线y=x-4与x轴交于点A,直线y=ax+b也经过点A,且与y轴的正半轴交于点B,若∠1=105°,则直线AB的解析式为( )| A. | y=-$\frac{1}{2}$x+2 | B. | y=$\frac{1}{2}$x+2 | C. | y=$\frac{\sqrt{3}}{3}$x-$\frac{4\sqrt{3}}{3}$ | D. | y=-$\frac{\sqrt{3}}{3}$x+$\frac{4\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=2x2+1 | B. | y=2(x-2)2+2 | C. | y=2(x-2)2 | D. | y=2x2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com